题目内容
10．已知集合A={x∈N*|x2-5x-6＜0}，集合B={x|3≤x≤6}，则A∩B=（ ）| A． | {1，2，3，4，5} | B． | {3，4，5} | C． | {3，4，5，6} | D． | {1，2，3，4，5，6} |
分析 解不等式求出集合A，根据交集的定义写出A∩B．
解答 解：集合A={x∈N*|x2-5x-6＜0}
={x∈N*|-1＜x＜6}
={1，2，3，4，5}，
集合B={x|3≤x≤6}，
所以A∩B={3，4，5}．
故选：B．
点评 本题考查了解一元二次不等式与交集的基本运算问题，是基础题．
练习册系列答案
相关题目
16．一个几何体的三视图如图所示，则该几何体的体积是（ ）
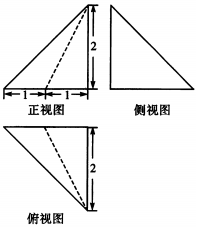
| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{4}{3}$ | D． | $\frac{8}{3}$ |
1．在△ABC中，a，b，c分别为∠A、∠B、∠C、的对边，若a+c=2b，且$sinB=\frac{4}{5}$，当△ABC的面积为$\frac{3}{2}$时，则b=（ ）
| A． | $\frac{{1+\sqrt{3}}}{2}$ | B． | 2 | C． | 4 | D． | 2+$\sqrt{3}$ |
19．（理）若a=${∫}_{\frac{π}{2}}^{2}$sinxdx，b=∫01cosxdx，则a与b的关系是（ ）
| A． | a+b=0 | B． | a＞b | C． | a＜b | D． | a=b |
20．PA、PB、PC是从P点引出的三条射线，每两条的夹角为60°，则直线PC与平面APB所成角的余弦值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{{\sqrt{3}}}{3}$ | D． | $\frac{{\sqrt{3}}}{2}$ |