题目内容
2.已知命题p:方程x2-2x+m=0有两个不相等的实数根;命题q:关于x的函数y=(m+2)x-1是R上的单调增函数,若“p或q”是真命题,“p且q”是假命题,则实数m的取值范围为(-∞,-2]∪[1,+∞).分析 求出命题p为真时m的取值范围,再求出命题q为真时m的取值范围,
根据“p或q”是真命题,“p且q”是假命题,得出p与q一真一假,从而求出m的取值范围.
解答 解:命题p:方程x2-2x+m=0有两个不相等的实数根,
∴△=4-4m>0,解得m<1;
命题q:函数y=(m+2)x-1是R上的单调增函数,
∴m+2>0,解得m>-2;
若“p或q”是真命题,“p且q”是假命题,
∴p与q一真一假;
当p真q假时,$\left\{\begin{array}{l}{m<1}\\{m≤-2}\end{array}\right.$,解得m≤-2.
当q真p假时,$\left\{\begin{array}{l}{m≥1}\\{m>-2}\end{array}\right.$,解得m≥1.
∴实数m的取值范围是m≤-2或m≥1.
故答案为:(-∞,-2]∪[1,+∞).
点评 本题考查了简易逻辑的判定语句一元二次方程的实数根与一次函数的单调性问题,属于基础题.

练习册系列答案
相关题目
10.已知集合A={x∈N*|x2-5x-6<0},集合B={x|3≤x≤6},则A∩B=( )
| A. | {1,2,3,4,5} | B. | {3,4,5} | C. | {3,4,5,6} | D. | {1,2,3,4,5,6} |
17.某港口水的深度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t).下面是某日水深的数据:
经长期观察,y=f(t)的曲线可以近似地看成函数y=Asinωt+b的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).某船吃水程度(船底离水面的距离)为6.5m,如果该船希望在同一天内安全进出港,请问,它最多能在港内停留( )小时(忽略进出港所需的时间).
| t/h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/m | 10 | 13 | 10 | 7 | 10 | 13 | 10 | 7 | 10 |
| A. | 6 | B. | 12 | C. | 16 | D. | 18 |
7.已知tanα=$\sqrt{2}$,α为第三象限角,则$\sqrt{2}$sinα+cosα=( )
| A. | -$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | -$\sqrt{3}$ | D. | -2$\sqrt{3}$ |
14.设a>0,b>0,若a+b=1,则$\frac{1}{a}+\frac{4}{b}$的最小值为( )
| A. | 8 | B. | 9 | C. | 4 | D. | $\frac{1}{4}$ |
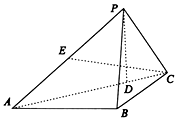 如图,在三棱锥P-ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°,$PC=\sqrt{3}$,D为AC上一点,且AD=3DC.
如图,在三棱锥P-ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°,$PC=\sqrt{3}$,D为AC上一点,且AD=3DC.