题目内容
20.PA、PB、PC是从P点引出的三条射线,每两条的夹角为60°,则直线PC与平面APB所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 在PC上任取一点D并作PO⊥平面APB,则∠DPO就是直线PC与平面APB所成的角,由此能求出直线PC与平面PAB所成角的余弦值.
解答 解:在PC上任取一点D并作PO⊥平面APB,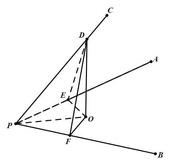
则∠DPO就是直线PC与平面APB所成的角.
过点O作OE⊥PA,OF⊥PB,
∵DO⊥平面APB,∴DE⊥PA,DF⊥PB.
△DEP≌△DFP,∴EP=FP,∴△OEP≌△OFP,
∵∠APC=∠BPC=60°,∴点O在∠APB的平分线上,即∠OPE=30°.
设PE=1,∵∠OPE=30°,∴OP=$\frac{1}{cos30°}$=$\frac{2\sqrt{3}}{3}$,
在直角△PED中,∠DPE=60°,PE=1,则PD=2.
在直角△DOP中,OP=$\frac{2\sqrt{3}}{3}$,PD=2.则cos∠DPO=$\frac{OP}{PD}$=$\frac{\sqrt{3}}{3}$.
即直线PC与平面PAB所成角的余弦值是 $\frac{\sqrt{3}}{3}$.
故选:C.
点评 本题考查线面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
10.已知集合A={x∈N*|x2-5x-6<0},集合B={x|3≤x≤6},则A∩B=( )
| A. | {1,2,3,4,5} | B. | {3,4,5} | C. | {3,4,5,6} | D. | {1,2,3,4,5,6} |
8.$\frac{1-2i}{2+i}$=( )
| A. | -i | B. | i | C. | 1 | D. | 2-i |
15.在直三棱柱ABC-A1B1C1中,AB=BC=1,AC=$\sqrt{2}$,BB1=2,点M为BB1的中点,则点A到平面A1CM距离为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
5.若双曲线$\frac{{x}^{2}}{16+k}$-$\frac{{y}^{2}}{8-k}$=1(-16<k<8)的一条渐近线方程是y=-$\sqrt{3}$x,点P(3,y0)与点Q是双曲线上关于坐标原点对称的两点,则四边形F1QF2P的面积是.
| A. | 12$\sqrt{6}$ | B. | 6$\sqrt{6}$ | C. | 12$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
10.在平面直角坐标系中,矩形ABCD的对角线所在的直线相较于(0,1),若边AB所在的直线的方程为x-2y-2=0,则圆(x-1)2+(y-1)2=9被直线CD所截的弦长为( )
| A. | 3 | B. | $2\sqrt{3}$ | C. | 4 | D. | $3\sqrt{2}$ |
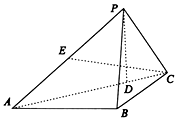 如图,在三棱锥P-ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°,$PC=\sqrt{3}$,D为AC上一点,且AD=3DC.
如图,在三棱锥P-ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°,$PC=\sqrt{3}$,D为AC上一点,且AD=3DC.