题目内容
1.在△ABC中,a,b,c分别为∠A、∠B、∠C、的对边,若a+c=2b,且$sinB=\frac{4}{5}$,当△ABC的面积为$\frac{3}{2}$时,则b=( )| A. | $\frac{{1+\sqrt{3}}}{2}$ | B. | 2 | C. | 4 | D. | 2+$\sqrt{3}$ |
分析 由a+c=2b,且$sinB=\frac{4}{5}$,可得B为锐角,cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{3}{5}$.由题意可得:$\frac{3}{2}$=$\frac{1}{2}$acsinB=$\frac{1}{2}$ac×$\frac{4}{5}$,化为:ac=$\frac{15}{4}$,又b2=a2+c2-2ac×$\frac{3}{5}$,a+c=2b,联立解得b.
解答 解:由a+c=2b,且$sinB=\frac{4}{5}$,可得B为锐角,cosB=$\sqrt{1-si{n}^{2}B}$=$\frac{3}{5}$.
由题意可得:$\frac{3}{2}$=$\frac{1}{2}$acsinB=$\frac{1}{2}$ac×$\frac{4}{5}$,化为:ac=$\frac{15}{4}$,
又b2=a2+c2-2ac×$\frac{3}{5}$,a+c=2b,
联立解得b=2,
故选:B.
点评 本题考查了三角形面积计算公式、余弦定理、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知命题p:?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0,命题q:实数x,y∈R,若x+y>2,则x>1或y>1;若p∧q为假命题,则( )
| A. | 函数f(x)为R上增函数 | B. | 函数f(x)为R上减函数 | ||
| C. | 函数f(x)在R上单调性不确定 | D. | 命题q为假命题 |
6.函数f(x)=cos4x•cos2x•cosx•sinx的最大值和最小正周期依次为 ( )
| A. | $\frac{1}{8};\frac{π}{4}$ | B. | $\frac{1}{4};\frac{π}{2}$ | C. | $\frac{1}{2};π$ | D. | 1;2π |
10.已知集合A={x∈N*|x2-5x-6<0},集合B={x|3≤x≤6},则A∩B=( )
| A. | {1,2,3,4,5} | B. | {3,4,5} | C. | {3,4,5,6} | D. | {1,2,3,4,5,6} |
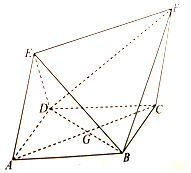 如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.
如图,四边形ABCD为菱形,四边形ACEF为平行四边形,设BD与AC相交于点G,AB=BD=2,AE=$\sqrt{3}$,∠EAD=∠EAB.