题目内容
函数y=
的递减区间是 .
| 2 |
| x+1 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:用单调性的定义来判断函数f(x)在(-1,+∞)和(-∞,-1)上是减函数,从而得单调减区间.
解答:
解:∵函数y=
,x≠-1;
∴任取x1、x2∈(-1,+∞),且x1<x2,
则f(x1)-f(x2)=
-
=
;
∵-1<x1<x2,
∴2(x2-x1)>0,(x1+1)(x2+1)>0,
∴f(x1)>f(x2);
∴f(x)在(-1,+∞)上是减函数;
同理,f(x)在(-∞,-1)上也是减函数;
∴f(x)的递减区间是(-∞,-1),(-1,+∞).
故答案为:(-∞,-1),(-1,+∞).
| 2 |
| x+1 |
∴任取x1、x2∈(-1,+∞),且x1<x2,
则f(x1)-f(x2)=
| 2 |
| x1+1 |
| 2 |
| x2+1 |
=
| 2(x2-x1) |
| (x1+1)(x2+1) |
∵-1<x1<x2,
∴2(x2-x1)>0,(x1+1)(x2+1)>0,
∴f(x1)>f(x2);
∴f(x)在(-1,+∞)上是减函数;
同理,f(x)在(-∞,-1)上也是减函数;
∴f(x)的递减区间是(-∞,-1),(-1,+∞).
故答案为:(-∞,-1),(-1,+∞).
点评:本题考查了求函数单调区间的问题,解题时应结合单调性的定义进行判断,是基础题.

练习册系列答案
相关题目
已知函数y=f(x)是定义在R上的奇函数,且当x∈(-∞,0)时不等式f(x)+xf′(x)<0成立,若a=3•f(3),b=f(1),c=-2f(-2).则a,b,c的大小关系是( )
| A、a>b>c |
| B、c>a>b |
| C、c>b>a |
| D、a>c>b |
已知集合A={x|x>4或x<-1},B={x|ax-1>0},若A∪B=A,则实数a的取值范围是( )
A、(0,
| ||
B、(-1,0)∪(0,
| ||
C、(-1,
| ||
D、[-1,
|
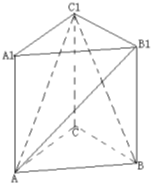 (文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.
(文)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2.