题目内容
已知向量
=(1,x),
=(x2,2),且
⊥
,则实数x的值为 .
| a |
| b |
| a |
| b |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:由已知得
•
=x2+2x=0,由此能求出x的值.
| a |
| b |
解答:
解:∵
=(1,x),
=(x2,2),且
⊥
,
∴
•
=x2+2x=0,
解得x=0,或x=-2.
故答案为:-2或0.
| a |
| b |
| a |
| b |
∴
| a |
| b |
解得x=0,或x=-2.
故答案为:-2或0.
点评:本题考查实数值的求法,是基础题,解题时要注意向量垂直的性质的合理运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
若关于x,y的不等式组
(k是常数)所表示的平面区域的边界是一个直角三角形,则k的值为( )
|
| A、0或1 | B、1或2 |
| C、0或2 | D、0或-1 |

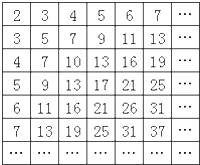 表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij.则
表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij.则