题目内容
若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k=( )
| A、-1 | B、0 | C、1 | D、2 |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出原函数的导函数,得到函数在x=1时的导数,由导数对于0求得k的值.
解答:
解:∵y=kx+lnx,
∴y′=k+
,
则y′|x=1=k+1.
又曲线y=kx+lnx在点(1,k)处的切线平行于x轴,
∴k+1=0,即k=-1.
故选:A.
∴y′=k+
| 1 |
| x |
则y′|x=1=k+1.
又曲线y=kx+lnx在点(1,k)处的切线平行于x轴,
∴k+1=0,即k=-1.
故选:A.
点评:本题考查了利用导数研究过曲线上某点处的切线方程,考查了基本初等函数的导数公式,是中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
最小二乘法的原理是( )
A、使得
| |||
B、使得
| |||
C、使得
| |||
D、使得
|
在等比数列{an}中,an>0,且a2a4+2a3a5+a4a6=25,那么a3+a5=( )
| A、5 | B、10 | C、15 | D、20 |
数列{an}满足an+2-2an+1+an=0(n∈N*),a1=31,a2=29,则该数列中相邻两项的乘积是负数的是( )
| A、a14a15 |
| B、a15a16 |
| C、a16a17 |
| D、a17a18 |
若关于x,y的不等式组
(k是常数)所表示的平面区域的边界是一个直角三角形,则k的值为( )
|
| A、0或1 | B、1或2 |
| C、0或2 | D、0或-1 |
下列函数中,以
为最小正周期的偶函数是( )
| π |
| 2 |
| A、y=sin2x+cos2x | ||
| B、y=sin2xcos2x | ||
C、y=cos(4x+
| ||
| D、y=sin22x-cos22x |
设{an}是集合{2s+2t|0≤s<t,且s,t∈Z}中所有的数从小到大排成的数列,则a50的值是( )
| A、1024 | B、1032 |
| C、1040 | D、1048 |
给出下列两个命题:命题p:
是有理数;命题q:若a>0,b>0,则方程ax2+by2=1表示椭圆.那么下列命题中为真命题的是( )
| 2 |
| A、p∧q | B、p∨q |
| C、(﹁p)∧q | D、(﹁p)∨q |
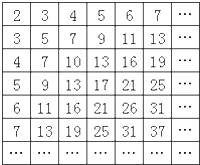 表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij.则
表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij.则