题目内容
x、y∈R,
-
=
,则xy= .
| x |
| 1-i |
| y |
| 1-2i |
| 5 |
| 1-3i |
考点:复数代数形式的乘除运算,复数相等的充要条件
专题:数系的扩充和复数
分析:利用复数的运算法则、共轭复数的定义、复数相等即可得出.
解答:
解:∵x、y∈R,
-
=
,
∴
-
=
,
化为
-
=
,
∴5(x+xi)-2(y+2yi)=5(1+3i),
化为5x-2y-5+(5x-4y-15)i=0,
∴
,解得
.
∴xy=5.
故答案为:5.
| x |
| 1-i |
| y |
| 1-2i |
| 5 |
| 1-3i |
∴
| x(1+i) |
| (1-i)(1+i) |
| y(1+2i) |
| (1-2i)(1+2i) |
| 5(1+3i) |
| (1-3i)(1+3i) |
化为
| x+xi |
| 2 |
| y+2yi |
| 5 |
| 1+3i |
| 2 |
∴5(x+xi)-2(y+2yi)=5(1+3i),
化为5x-2y-5+(5x-4y-15)i=0,
∴
|
|
∴xy=5.
故答案为:5.
点评:本题考查了复数的运算法则、共轭复数的定义、复数相等,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


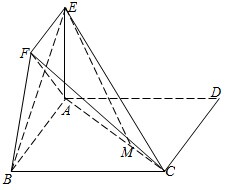 如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1,
如图,四边形ABCD为正方形,EA⊥平面ABCD,EF∥AB,AB=4,AE=2,EF=1,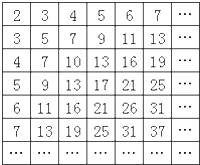 表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij.则
表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij.则