题目内容
若函数f(x)=
在(0,3)上单调递增,则实数a的取值范围为 .
| x |
| x2+a |
考点:函数单调性的性质
专题:函数的性质及应用
分析:若f(x)=
在(0,3)上单调递增,则f′(x)=
≥0在(0,3)上恒成立,则-x2+a≥0在(0,3)上恒成立,则a≥x2在(0,3)上恒成立,进而得到实数a的取值范围.
| x |
| x2+a |
| -x2+a |
| (x2+a)2 |
解答:
解:∵f(x)=
在(0,3)上单调递增,
∴f′(x)=
≥0在(0,3)上恒成立,
∴-x2+a≥0在(0,3)上恒成立,
∴a≥x2在(0,3)上恒成立,
∴a≥9,
∴实数a的取值范围为[9,+∞),
故答案为:[9,+∞)
| x |
| x2+a |
∴f′(x)=
| -x2+a |
| (x2+a)2 |
∴-x2+a≥0在(0,3)上恒成立,
∴a≥x2在(0,3)上恒成立,
∴a≥9,
∴实数a的取值范围为[9,+∞),
故答案为:[9,+∞)
点评:本题考查的知识点是函数单调性的性质,其中将函数的单调性转化为恒成立问题,进而转化为最值问题是解答的关键.

练习册系列答案
相关题目
最小二乘法的原理是( )
A、使得
| |||
B、使得
| |||
C、使得
| |||
D、使得
|
下列函数中,以
为最小正周期的偶函数是( )
| π |
| 2 |
| A、y=sin2x+cos2x | ||
| B、y=sin2xcos2x | ||
C、y=cos(4x+
| ||
| D、y=sin22x-cos22x |
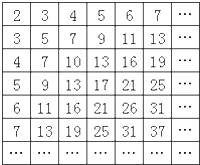 表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij.则
表中的数阵为“森德拉姆数筛”,其特点是每行每列都成等差数列,记第i行第j列的数为aij.则