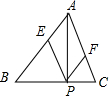
题目内容
已知△ABC中tanA=3，
=
+
，
=λ（
+
）且
∥
，则tanB=（ ）
| AP |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
| AD |
| ||
|
|
| ||
|
|
| AP |
| AD |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由
=λ（
+
）可得
•
=λ(
+
)=0，可得
⊥
．又
∥
，可得
⊥
．由
=
+
，不妨设PC=1，则BP=2．AP=x．可得tan∠BAP=
，tan∠CAP=
．利用tan∠BAC=tan（∠BAP+∠CAP）=
=3，解得x．在△ABP中，利用tanB=
即可得出．
| AD |
| ||
|
|
| ||
|
|
| AD |
| CB |
| ||||
|
|
| ||||
|
|
| AD |
| CB |
| AP |
| AD |
| AP |
| BC |
| AP |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
| 2 |
| x |
| 1 |
| x |
| tan∠BAP+tan∠CAP |
| 1-tan∠BAPtan∠CAP |
| AP |
| BP |
解答：
解：∵
•
=|
||
|cosB，
•
=|
||
|cosC，
=λ（
+
）
∴
•
=λ(
+
)=λ(|
|-|
|)=0，
∴
⊥
．
∵
∥
，
∴
⊥
．
∵
=
+
，
∴设PC=1，则BP=2．AP=x．
则tan∠BAP=
，tan∠CAP=
．
∴tan∠BAC=tan（∠BAP+∠CAP）=
=
=3，
化为x2-x-2=0，
解得x=2．
在△ABP中，tanB=
=1，
故选：C．
| AB |
| CB |
| AB |
| CB |
| AC |
| BC |
| AC |
| BC |
| AD |
| ||
|
|
| ||
|
|
∴
| AD |
| CB |
| ||||
|
|
| ||||
|
|
| CB |
| BC |
∴
| AD |
| CB |
∵
| AP |
| AD |
∴
| AP |
| BC |
∵
| AP |
| 1 |
| 3 |
| AB |
| 2 |
| 3 |
| AC |
∴设PC=1，则BP=2．AP=x．
则tan∠BAP=
| 2 |
| x |
| 1 |
| x |
∴tan∠BAC=tan（∠BAP+∠CAP）=
| tan∠BAP+tan∠CAP |
| 1-tan∠BAPtan∠CAP |
| ||||
1-
|
化为x2-x-2=0，
解得x=2．
在△ABP中，tanB=
| AP |
| BP |
故选：C．
点评：本题考查了向量的数量积运算性质、向量共线定理、向量垂直与数量积的关系、两角和差的正切公式、直角三角形的边角公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
下列函数，是周期函数的为（ ）
| A、y=sin|x| |
| B、y=cos|x| |
| C、y=tan|x| |
| D、y=（x-1）0 |
如图，在平面直角坐标系xOy中，点A位椭圆E：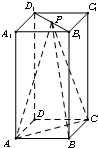
如图，在长方体ABCD-A1B1C1D1中，AB=BC=2，AA1=4，P为线段B1D1上一点．