题目内容
已知以下四个函数:①y=kx(k∈R);②y=xn(n为奇数);③y=x2cosx;④y=2x+sinx.其中图象可以平分圆O:x2+y2=1的面积的函数个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:利用圆的对称性,判断函数的奇偶性然后推出结果即可.
解答:
解:因为圆O:x2+y2=1的图象关于坐标轴以及原点对称,要使函数的图象平方圆的面积,只需函数是奇函数,
因为:①y=kx(k∈R);是奇函数,图象可以平分圆O:x2+y2=1的面积.满足题意.
②y=xn(n为奇数);是奇函数,图象可以平分圆O:x2+y2=1的面积.满足题意.
③y=x2cosx;是偶函数,图象不平分圆O:x2+y2=1的面积.不满足题意.
④y=2x+sinx.是奇函数,图象可以平分圆O:x2+y2=1的面积.满足题意.
故选:C.
因为:①y=kx(k∈R);是奇函数,图象可以平分圆O:x2+y2=1的面积.满足题意.
②y=xn(n为奇数);是奇函数,图象可以平分圆O:x2+y2=1的面积.满足题意.
③y=x2cosx;是偶函数,图象不平分圆O:x2+y2=1的面积.不满足题意.
④y=2x+sinx.是奇函数,图象可以平分圆O:x2+y2=1的面积.满足题意.
故选:C.
点评:本题考查函数的奇偶性没有的图形的性质,考查分析问题解决问题的能力.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
在△ABC中,D为BC上一点,BD=
DC,∠ADB=120°,AD=2,若△ADC的面积为3-
,则∠ABC=( )
| 1 |
| 2 |
| 3 |
| A、30° | B、60° |
| C、15° | D、45° |
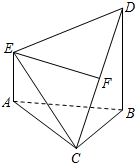 如图,在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,BD∥AE,BD=2AE.
如图,在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,BD∥AE,BD=2AE.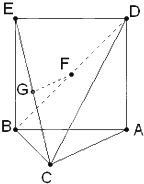 三角形ABC中,AC=BC=
三角形ABC中,AC=BC=