题目内容
求满足条件{2，3}⊆M⊆{2，3，4，5}的所有集合M．
考点：子集与真子集
专题：集合
分析：明确集合包含关系与真包含关系的区别，能正确的找出集合M的元素是此题的关键．
解答：
解：{2，3}⊆M⊆{2，3，4，5}
∴2，3∈M，
∴满足条件的M有{2，3}，{2，3，4}，{2，3，5}，{2，3，4，5}．
∴2，3∈M，
∴满足条件的M有{2，3}，{2，3，4}，{2，3，5}，{2，3，4，5}．
点评：本题考察了集合的关系，关键是列举，属于基础题．
练习册系列答案
相关题目
直线y=a分别与曲线y=2（x+1），y=x+lnx交于A、B，则|AB|的最小值为（ ）
| A、3 | ||||
| B、2 | ||||
C、
| ||||
D、
|
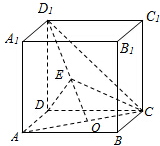如图，在正方体ABCD-A1B1C1D1中，O是AC的中点，E是线段D1O上一点，且|D1E|=λ|EO|．
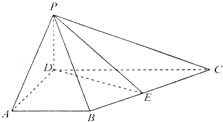如图，ABCD为梯形，PD⊥平面ABCD，AB∥CD，∠BAD=∠ADC=90°，DC=2AB=2a，DA=
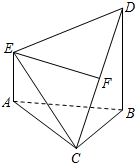如图，在四棱锥C-ABDE中，F为CD的中点，DB⊥平面ABC，BD∥AE，BD=2AE．