题目内容
已知空间四边形OABC,棱OA,OB,OC相互垂直,且OA=OB=BC=1,N是OC的中点,点M在AB上,且MN⊥AB,求MN与AB的比值.
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:构造棱长为1的正方体DEBF-PAOC,OA,OB,OC是正方体中过同一顶点O的三条棱,以D为原点,DE为x轴,DF为y轴,DP为z轴,建立空间直角坐标系,利用向量法能求出MN与AB的比值.
解答:
解: 构造如图所示的棱长为1的正方体DEBF-PAOC,
构造如图所示的棱长为1的正方体DEBF-PAOC,
OA,OB,OC是正方体中过同一顶点O的三条棱,
以D为原点,DE为x轴,DF为y轴,DP为z轴,
建立空间直角坐标系,
则A(1,0,1),B(1,1,0),N(
,1,1),
=(0,1,-1),
设
=t
,0≤t≤1,M(1,a,b),
则(0,a,b-1)=(0,t,-t),∴a=t,b=1-t,
∴M(1,t,1-t),∴
=(-
,1-t,t),
∵MN⊥AB,∴
•
=1-t-t=0,解得t=
,
∴M(1,
,
),|
|=
=
,
又|
|=
=
,
∴MN与AB的比值为
=
=
.
 构造如图所示的棱长为1的正方体DEBF-PAOC,
构造如图所示的棱长为1的正方体DEBF-PAOC,OA,OB,OC是正方体中过同一顶点O的三条棱,
以D为原点,DE为x轴,DF为y轴,DP为z轴,
建立空间直角坐标系,
则A(1,0,1),B(1,1,0),N(
| 1 |
| 2 |
| AB |
设
| AM |
| AB |
则(0,a,b-1)=(0,t,-t),∴a=t,b=1-t,
∴M(1,t,1-t),∴
| MN |
| 1 |
| 2 |
∵MN⊥AB,∴
| MN |
| AB |
| 1 |
| 2 |
∴M(1,
| 1 |
| 2 |
| 1 |
| 2 |
| MN |
|
| ||
| 2 |
又|
| AB |
| 0+1+1 |
| 2 |
∴MN与AB的比值为
|
| ||
|
|
| ||
2
|
| ||
| 4 |
点评:本题考查两条线段的比值的求法,是中档题,解题时要认真审题,注意构造法的合理运用,注意空间向量在立体几何中的应用,意在考查方程思想、等价转化思想等数学思想方法和考生的空间想象能力、逻辑推理能力和运算求解能力.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知函数f(x),g(x)均为[a,b]上的可导函数,在[a,b]上连续且f′(x)<g′(x),则f(x)-g(x)的最大值为( )
| A、f(a)-g(a) |
| B、f(b)-g(b) |
| C、f(a)-g(b) |
| D、f(b)-g(a) |
设F1、F2为椭圆C:
+
=1(a>b>0)的左、右焦点,直线l过焦点F2且与椭圆交于A,B两点,若△ABF1构成以A为直角顶点的等腰直角三角形,设椭圆离心率为e,则e2=( )
| x2 |
| a2 |
| y2 |
| b2 |
A、2-
| ||
B、3-
| ||
C、11-6
| ||
D、9-6
|
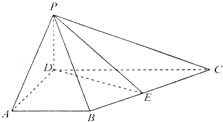 如图,ABCD为梯形,PD⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=
如图,ABCD为梯形,PD⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=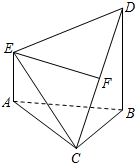 如图,在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,BD∥AE,BD=2AE.
如图,在四棱锥C-ABDE中,F为CD的中点,DB⊥平面ABC,BD∥AE,BD=2AE.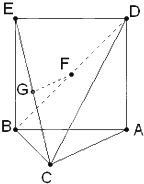 三角形ABC中,AC=BC=
三角形ABC中,AC=BC=