题目内容
下列函数，是周期函数的为（ ）
| A、y=sin|x| |
| B、y=cos|x| |
| C、y=tan|x| |
| D、y=（x-1）0 |
考点：三角函数的周期性及其求法
专题：函数的性质及应用
分析：由条条件根据三角函数的图象特征，三角函数的周期性，可得结论．
解答：
解：根据函数y=sin|x|的图象特征，可得它不是周期函数．
根据y=cos|x|的图象特征可得它的周期为2π，
根据函数y=tan|x|的图象特征，可得它不是周期函数．
根据函数y=（x-1）0的图象特征，可得它不是周期函数．
故选：B．
根据y=cos|x|的图象特征可得它的周期为2π，
根据函数y=tan|x|的图象特征，可得它不是周期函数．
根据函数y=（x-1）0的图象特征，可得它不是周期函数．
故选：B．
点评：本题主要考查三角函数的图象特征，三角函数的周期性，属于基础题．
练习册系列答案
相关题目
已知f（x）=x3-2x2+x+6，则f（x）在点P（-1，2）处的切线与坐标轴围成的三角形面积等于（ ）
| A、4 | ||
| B、5 | ||
C、
| ||
D、
|
直线y=a分别与曲线y=2（x+1），y=x+lnx交于A、B，则|AB|的最小值为（ ）
| A、3 | ||||
| B、2 | ||||
C、
| ||||
D、
|
己知命题p：“a＞b”是“2a＞2b”的充要条件；q：?x∈R，|x+l|≤x，则（ ）
| A、￢p∨q为真命题 |
| B、p∧￢q为假命题 |
| C、p∧q为真命题 |
| D、p∨q为真命题 |
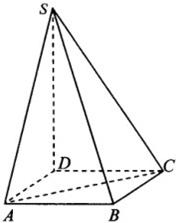如图，设四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=2a，AD=