题目内容
已知f(x)=|x2-9|+x2+kx,若关于x的方程f(x)=0在(0,4)上有两个实数解,则k的取值范围是 .
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:转化为函数g(x)=|x2-9|+x2=
与h(x)=-kx的图象,运用图象解决问题.
|
解答:
解:方程f(x)=0可以转化为|x2-9|+x2=-kx,记g(x)=|x2-9|+x2,则f(x)=0在(0,4)上有两个实数解,
可以转化为函数g(x)=|x2-9|+x2=
与h(x)=-kx的图象,

结合图象和特殊点A(3,9),B(4,23)
可知k∈(-
,-3;
故答案为:(-
,-3).
可以转化为函数g(x)=|x2-9|+x2=
|

结合图象和特殊点A(3,9),B(4,23)
可知k∈(-
| 23 |
| 4 |
故答案为:(-
| 23 |
| 4 |
点评:本题考查了二次函数的图象,运用图象解决问题,属于中档题.

练习册系列答案
相关题目
一物体在力F(x)=
(单位:N)的作用下沿与力F(x)相同的方向运动了4米,力F(x)做功为( )
|
| A、44J | B、46J |
| C、48J | D、50J |
已知实数x,y满足约束条件
,目标函数z=x+y,则当z=3时,
的取值范围是( )
|
| y |
| x |
A、[
| ||
B、[
| ||
C、[1,
| ||
| D、[2,4] |
已知命题p1:存在x0∈R,使得x02+x0+1<0成立;p2:对任意的x∈[1,2],x2-1≥0.以下命题为真命题的是( )
| A、¬p1∧¬p2 |
| B、p1∨¬p2 |
| C、¬p1∧p2 |
| D、p1∧p2 |
已知角α的终边上一点P(x,-2),且cosα=-
.则x=( )
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、±
|
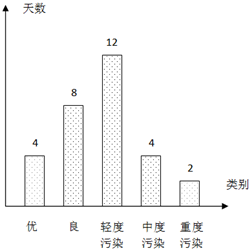 经过对某市空气质量指数进行一个月(30天)监测,获得数据后得到条形图统计图:
经过对某市空气质量指数进行一个月(30天)监测,获得数据后得到条形图统计图: