Question

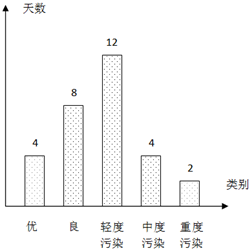经过对某市空气质量指数进行一个月（30天）监测，获得数据后得到条形图统计图：

空气质量指数	0～35	35～75	75～115	115～150	150～250	≥250
空气质量类别	优	良	轻度污染	中度污染	重度污染	严重污染

（Ⅰ）估计某市一个月内空气受到污染的概率（规定：空气质量指数大于或等于75，空气受到污染）； 
（Ⅱ）在空气质量类别为“良”、“轻度污染”的监测数据中用分层抽样方法抽取一个容量为5的样本，若在这5数据中任取2个数据，求这2个数据所对应的空气质量类别不都是轻度污染的概率．

Answer 1

考点：频率分布表

专题：概率与统计

分析：（Ⅰ）根据表中数据即可估计该市一个月内空气受到污染的概率； 
（Ⅱ）求出空气质量类别为“良”与“轻度污染”的天数，再求用分层抽样方法抽取的样本组成，用列举法求出基本事件，求出对应的概率．

解答： 解：（Ⅰ）根据表中数据估计该市一个月内空气受到污染的概率是
P=

12+4+2

30

=0.6； 
（Ⅱ）空气质量类别为“良”的天数是8，“轻度污染”的天数是12；
用分层抽样方法抽取一个容量为5的样本，空气质量类别为“良”的是2，记为A、B；
“轻度污染”的是3，记为a、b、c；
在这5数据中任取2个数据，基本事件是AB，Aa，Ab，Ac，Ba，Bb，Bc，ab，ac，bc共10个；
则这2个数据所对应的空气质量类别不都是轻度污染的基本事件是AB，Aa，Ab，Ac，Ba，Bb，Bc共7个，
∴概率为P=

7

10

=0.7．

点评：本题考查了频率分布直方图的应用问题，也考查了古典概型的应用问题，是基础题．