题目内容
 为了解某校高三学生的视力情况,随机抽查了该校50名高三学生,得到如图所示的频率分布直方图.
为了解某校高三学生的视力情况,随机抽查了该校50名高三学生,得到如图所示的频率分布直方图.(Ⅰ)求图中x的值;
(Ⅱ)从视力不低于1.0的学生中随机选取2人,设这2人中视力不低于1.2的人数为ξ,求ξ的数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由频率分布直方图,能求出x.
(Ⅱ)由已知得ξ=0,1,2,分别求出相应的概率,由此能求出ξ的数学期望.
(Ⅱ)由已知得ξ=0,1,2,分别求出相应的概率,由此能求出ξ的数学期望.
解答:
(本小题满分13分)
解:(Ⅰ)由频率分布直方图,得:
x=[1-(0.3×3+0.6+2.5)×0.2]÷0.2=1.…(6分)
(Ⅱ)由已知得ξ=0,1,2,
由频率分布直方图,得视力不低于1.0的学生有10人,
视力不低于1.2的人数为3人,
∴P(ξ=0)=
=
,
P(ξ=1)=
=
,
P(ξ=2)=
=
,
∴ξ的分布列为:
Eξ=
+2•
=
…(13分)
解:(Ⅰ)由频率分布直方图,得:
x=[1-(0.3×3+0.6+2.5)×0.2]÷0.2=1.…(6分)
(Ⅱ)由已知得ξ=0,1,2,
由频率分布直方图,得视力不低于1.0的学生有10人,
视力不低于1.2的人数为3人,
∴P(ξ=0)=
| ||
|
| 15 |
| 26 |
P(ξ=1)=
| ||||
|
| 5 |
| 13 |
P(ξ=2)=
| ||
|
| 1 |
| 26 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 5 |
| 13 |
| 1 |
| 26 |
| 6 |
| 13 |
点评:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意排列组合知识的合理运用.

练习册系列答案
相关题目
 如图,在△OAB中,OA=4,OB=2,∠AOB=
如图,在△OAB中,OA=4,OB=2,∠AOB=| 2π |
| 3 |
| OP |
| OA |
| OB |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
、
、
为向量,下列结论:
①若
=
,
=
,则
=
;
②若
∥
,
∥
,则
∥
;
③|
•
|=|
|•|
|;
④若
•
=
•
,则
=
的逆命题.
其中正确的是( )
| a |
| b |
| c |
①若
| a |
| b |
| b |
| c |
| a |
| c |
②若
| a |
| b |
| b |
| c |
| a |
| c |
③|
| a |
| b |
| a |
| b |
④若
| a |
| b |
| a |
| c |
| b |
| c |
其中正确的是( )
| A、①② | B、①④ |
| C、①②③ | D、①②④ |
已知函数f(x)=x
(x>0),若对于任意α∈(0,
),都有f(tanα)+f(
)≥4cosβ(0≤β≤2π)成立,则β的取值范围是( )
| 1 |
| 2 |
| π |
| 2 |
| 1 |
| tanα |
A、[
| ||||
B、[
| ||||
C、[0,
| ||||
D、[0,
|
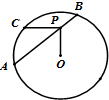 如图,AB是圆O的一条弦,点P是AB上一点,点C是圆O上一点,PC⊥OP,AP=4,PB=2,则PC=
如图,AB是圆O的一条弦,点P是AB上一点,点C是圆O上一点,PC⊥OP,AP=4,PB=2,则PC=