题目内容
在△ABC中，∠BAC=120°，AB=AC=2，（Ⅰ）求
| AB |
| BC |
（Ⅱ）设动点P在以A为圆心，AB为半径的劣弧BC上运动，求
| BP |
| CP |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（I）如图所示，利用数量积定义
•
=-
•
，即可得出；
（II）点P在以A为圆心，AB为半径的劣弧BC上运动，可得∠BPC=120°．利用数量积运算可得
•
=|
|•|
|cos120°=-
|
|•|
|≤0，即可得出．
| AB |
| BC |
| BA |
| BC |
（II）点P在以A为圆心，AB为半径的劣弧BC上运动，可得∠BPC=120°．利用数量积运算可得
| BP |
| CP |
| BP |
| CP |
| 1 |
| 2 |
| BP |
| CP |
解答：
解：（I）如图所示，
•
=-
•
=-2×2×cos120°=2．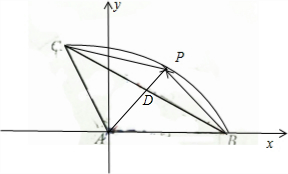
（II）点P在以A为圆心，AB为半径的劣弧BC上运动，∵∠BAC=120°，∴∠BPC=120°．
∴
•
=|
|•|
|cos120°=-
|
|•|
|≤0，
当点P取点B或C时，取等号．
∴
•
的最大值为0．
| AB |
| BC |
| BA |
| BC |
（II）点P在以A为圆心，AB为半径的劣弧BC上运动，∵∠BAC=120°，∴∠BPC=120°．
∴
| BP |
| CP |
| BP |
| CP |
| 1 |
| 2 |
| BP |
| CP |
当点P取点B或C时，取等号．
∴
| BP |
| CP |
点评：本题考查了数量积定义及其运算、圆的性质，考查了数形结合思想方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
四个小动物换座位，开始是鼠、猴、兔、猫分别坐1，2，3，4号位子上（如图），第一次前后排动物互换座位，第二次左右列动物互换座位，…，这样交替进行下去，那么第2015次互换座位后，小兔的座位对应的是（ ）
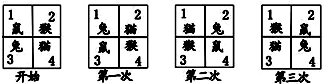
| A、编号1 | B、编号2 |
| C、编号3 | D、编号4 |
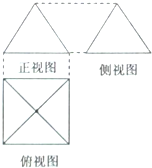如图，一个简单几何体三视图的正视图与侧视图都是边长为2的正三角形，其俯视图轮廓为正方形，则其体积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、4
|
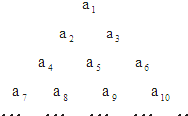已知数列{an}，an=3•(| 1 |
| 2 |
A、3•(
| ||
B、3•(
| ||
C、3•(
| ||
D、3•(
|
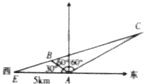如图，某海岛观察哨A测得在海岛北偏东60°的C处有一轮船，80分钟后测得船在海岛北偏西60°的B处，又过20分钟轮船到达位于海岛正西方且距离海岛5km的E港口，如果轮船始终作匀速直线运动，问船速多少？