题目内容
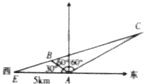如图，某海岛观察哨A测得在海岛北偏东60°的C处有一轮船，80分钟后测得船在海岛北偏西60°的B处，又过20分钟轮船到达位于海岛正西方且距离海岛5km的E港口，如果轮船始终作匀速直线运动，问船速多少？考点：解三角形的实际应用
专题：解三角形
分析：根据题意，可知BC=4BE，设BE=x海里，则BC=4x海里，在三角形BAE中，由正弦定理求得sinB，再在△ABC中，由正弦定理AB的长，在△ABE中，由余弦定理，得BE的长，从而得出船速即可．
解答：
解：依题意，在某海岛上一观察点A测得一轮船在海岛北偏东60°的B处，80分测得船在海岛北偏西60°的C处，过20分轮船到达了位于海岛正西方且距海岛5海里的E港口，轮船始终以匀速直线前进．
可知BC=4BE，
设BE=x海里，则BC=4x海里，
由已知，得∠CAE=150°，∠EAB=30°，
由正弦定理得
=
，即sinB=
=
=
，
在△ABC中，由正弦定理，得
=
，
∴AB=
，
在△AEB中，由余弦定理，得BE2=AB2+AE2-2AB•AE•cos30°=
+25-2×
×5×
=
，
即BE=
，
∴船速V=
=
=
=
（海里/小时）．
可知BC=4BE，
设BE=x海里，则BC=4x海里，
由已知，得∠CAE=150°，∠EAB=30°，
由正弦定理得
| EC |
| sin∠EAC |
| AE |
| sinB |
| AEsin∠EAC |
| EC |
5×
| ||
| 5x |
| 1 |
| 2x |
在△ABC中，由正弦定理，得
| 4x |
| sin120° |
| AB | ||
|
∴AB=
4
| ||
| 3 |
在△AEB中，由余弦定理，得BE2=AB2+AE2-2AB•AE•cos30°=
| 16 |
| 3 |
4
| ||
| 3 |
| ||
| 2 |
| 31 |
| 3 |
即BE=
| ||
| 3 |
∴船速V=
| S |
| t |
| BE | ||
|
| ||||
|
| 93 |
点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
在△ABC中，∠BAC=120°，AB=AC=2，函数f（x）=2x+2x-6的零点个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
抛物线y2=px（p＞0）的准线方程为x=-
，则p=（ ）
| 1 |
| 4 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|