题目内容
在棱长为1的正方体ABCD-A1B1C1D1中，点M是棱AD的中点，点P是线段CD1上的动点，点Q是线段CM上的动点，设直线PQ与平面ABCD所成的角为θ，则tanθ的最大值为 ．
考点：直线与平面所成的角
专题：空间位置关系与距离,空间角
分析：画出图形，不妨取D1为P，判断PQ与平面ABCD所成的角为θ的最大值位置，求解即可．
解答：
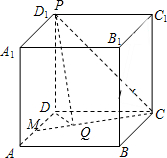解：如图，不妨取D1为P，直线PQ在平面D1MC中，直线PQ与平面ABCD所成的角的最大值就是二面角D1-MC-D的大小，过D作DQ⊥MC，连结D1Q，∠D1QD就是所求角θ．
正方体的棱长为1，MD=
，MC=
=
．
DQ=
=
=
．
tanθ=
=
．
故答案为：
．
解：如图，不妨取D1为P，直线PQ在平面D1MC中，直线PQ与平面ABCD所成的角的最大值就是二面角D1-MC-D的大小，过D作DQ⊥MC，连结D1Q，∠D1QD就是所求角θ．正方体的棱长为1，MD=
| 1 |
| 2 |
| MD2+DC2 |
| ||
| 2 |
DQ=
| MD•CD |
| MC |
1×
| ||||
|
| ||
| 5 |
tanθ=
| DQ |
| DD1 |
| ||
| 5 |
故答案为：
| ||
| 5 |
点评：本题考查直线与平面所成角的大小的求法，注意判断角的位置是解题的关键，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
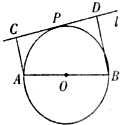如图，设AB为⊙O的任一条不与直线l垂直的直径，P是⊙O与l的公共点，AC⊥l，BD⊥l，垂足分别为C，D，且PC=PD．
在△ABC中，∠BAC=120°，AB=AC=2，