题目内容
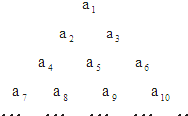 已知数列{an},an=3•(
已知数列{an},an=3•(| 1 |
| 2 |
A、3•(
| ||
B、3•(
| ||
C、3•(
| ||
D、3•(
|
考点:归纳推理,等比数列的通项公式
专题:等差数列与等比数列,推理和证明
分析:由题意和等差数列的前n项和公式求出前9行共有多少项,再由等比数列的通项公式求出A(10,8).
解答:
解:由题意得,第一行有1项,第二行有2项,…,第n行有n项,
则前9行共有1+2+3+…+9=
=45,
所以第10行第8个数是数列的第45+8=53项,
因为an=3•(
)n-1,所以A(10,8)=a53=3•(
)52,
故选:D.
则前9行共有1+2+3+…+9=
| 9(1+9) |
| 2 |
所以第10行第8个数是数列的第45+8=53项,
因为an=3•(
| 1 |
| 2 |
| 1 |
| 2 |
故选:D.
点评:本题考查了归纳推理,等差数列的前n项和公式,等比数列的通项公式,难点在于发现其中的规律,考查观察、分析、归纳能力.

练习册系列答案
相关题目
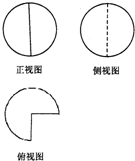 一个半径为1的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为( )
一个半径为1的球体经过切割后,剩余部分几何体的三视图如图所示,则该几何体的表面积为( )| A、16π | ||
| B、14π | ||
| C、4π | ||
D、
|
下列函数中,在定义域内既是奇函数又是减函数的是( )
| A、f(x)=log0.5x |
| B、f(x)=x3 |
| C、f(x)=x-1 |
| D、f(x)=-x3 |
 在△ABC中,∠BAC=120°,AB=AC=2,
在△ABC中,∠BAC=120°,AB=AC=2,