题目内容

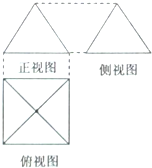如图，一个简单几何体三视图的正视图与侧视图都是边长为2的正三角形，其俯视图轮廓为正方形，则其体积是（　　）
A、
3
B、
4
3
3
C、
8
3
D、4
3
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：易得此几何体为四棱锥，利用相应的三角函数可得四棱锥的高，体积=
1
3
×底面积×高，把相关数值代入即可求解．
解答： 解：由主视图和左视图为等腰三角形可得此几何体为锥体，由俯视图为四边形可得此几何体为四棱锥，
∵主视图为边长为2的正三角形，
∴正三角形的高，也就是棱锥的高为
3
，俯视图的边长为2，
∴四棱锥的体积=
1
3
×2×2×
3
=
4
3
3
，
故选：B．
点评：解决本题的关键是得到该几何体的形状，易错是确定四棱锥的底面边长与高的大小．
练习册系列答案
相关题目
数列{an}中，a1=
1
2
，且(n+1)an+1=
nan
nan+1
（n∈N*），则数列{an}的前2014项的和为
 
．
△ABC中，a=2，C=
π
4
，cos
B
2
=
2
5
5
，则边c=
 
．
在△ABC中，若
AB
•
BC
=
BC
•
CA
=
CA
•
AB
，证明△ABC是等边三角形．
已知函数f（x）=
2
x
+alnx-2（a＞0）．
（Ⅰ）当a=1时，求函数y=f（x）的单调区间；
（Ⅱ）若对于?x∈（0，+∞）都有f（x）＞2（a-1）成立，试求a的取值范围．
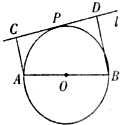如图，设AB为⊙O的任一条不与直线l垂直的直径，P是⊙O与l的公共点，AC⊥l，BD⊥l，垂足分别为C，D，且PC=PD．
（Ⅰ）求证：l是⊙O的切线；
（Ⅱ）若⊙O的半径OA=5，AC=4，求CD的长．
设向量
a
=（sinx，cosx），
b
=（cosx，cosx），x∈R，函数f（x）=
a
•
b
+1，使不等式f（x）≥
3
2
成立的x的取值集合为
 
．
在△ABC中，∠BAC=120°，AB=AC=2，
（Ⅰ）求
AB
•
BC
的值
（Ⅱ）设动点P在以A为圆心，AB为半径的劣弧BC上运动，求
BP
•
CP
的最大值．
函数f（x）=2x+2x-6的零点个数为（　　）
A、0B、1C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网