题目内容
直线l1：kx-y+2=0到直线l2：x+2y-3=0的角为45°，则k=（ ）
| A、-3 | B、-2 | C、2 | D、3 |
考点：两直线的夹角与到角问题
专题：直线与圆
分析：先根据根据直线的方程求斜率，再利用一条直线到另一条直线的角的计算公式求得k的值．
解答：
解：直线l1：kx-y+2=0的斜率为k，直线l2：x+2y-3=0的斜率为-
，
则根据一条直线到另一条直线的角为45°可得tan45°=
=1，
解得k=-3，
故选：A．
| 1 |
| 2 |
则根据一条直线到另一条直线的角为45°可得tan45°=
-
| ||
1+(-
|
解得k=-3，
故选：A．
点评：本题主要考查根据直线的方程求斜率，求一条直线到另一条直线的角的计算公式，属于中档题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
执行如图所示的程序框图，则输出的a的值为（ ）（注：“a=2”，即为“a←2”或为“a：=2”．）
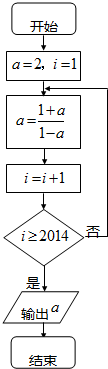
| A、2 | ||
B、
| ||
C、-
| ||
| D、-3 |
直线过点（-3，4），且在两坐标轴上的截距之和为12，则直线方程为（ ）
| A、4x-y+16=0 |
| B、x+3y-9=0 |
| C、4x-y+16=0或x+3y-9=0 |
| D、2x+y-16=0 |
复数
的虚部为（ ）
| -2i |
| 1-i |
| A、i | B、-i | C、1 | D、-1 |
已知△ABC三条边为a，b，c，
=(a，cos
)，
=(b，cos
)，
=(c，cos
)，且三个向量共线，则△ABC的形状是（ ）
| m |
| A |
| 2 |
| n |
| B |
| 2 |
| p |
| C |
| 2 |
| A、等腰三角形 |
| B、等边三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
函数f（x）=8+2x-x2的单调递增区间是（ ）
| A、[1，+∞） |
| B、（-∞，1] |
| C、[0，1] |
| D、（-∞，+∞ |