题目内容
15.阅读下列程序框图,输出的结果s的值为( )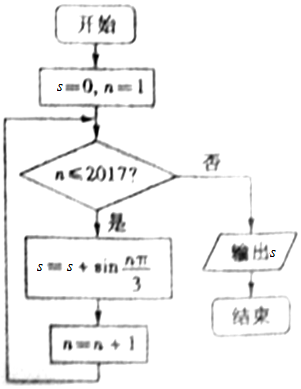
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
分析 由2017除以6余数为1,根据程序框图转化为一个关系式,利用特殊角的三角函数值化简,得出6个一循环,可得出所求的结果.
解答 解:∵2017÷6=336…1,
∴根据程序框图转化得:
sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+…+sin $\frac{2017π}{3}$=($\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$+0-$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$+0)+($\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$+0-$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$+0)+…+($\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$+0-$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{3}}{2}$+0)+$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$
故选:A.
点评 此题考查了运用诱导公式化简求值,循环结构,以及特殊角的三角函数值,认清程序框图,找出规律是解本题的关键.

练习册系列答案
相关题目
3.多项式(x2-2x-3)5展开式中含x项的系数为( )
| A. | 240 | B. | -810 | C. | 480 | D. | 600 |
10.若实数x,y满足x2+y2-2x+4y=0,则|x-2y+6|的最大值为( )
| A. | 11 | B. | 12 | C. | 16 | D. | 17 |
20.已知sinθ=$\frac{1}{3}$,θ∈(-$\frac{π}{2}$,$\frac{π}{2}$),则sin(π-θ)sin($\frac{π}{2}$-θ)的值为( )
| A. | $\frac{{2\sqrt{2}}}{9}$ | B. | $-\frac{{2\sqrt{2}}}{9}$ | C. | $\frac{1}{9}$ | D. | $-\frac{1}{9}$ |
7.底面是边长为1的正方形,侧面是等边三角形的四棱锥的外接球的体积为( )
| A. | $\frac{\sqrt{2}π}{3}$ | B. | $\frac{\sqrt{3}π}{3}$ | C. | $\frac{\sqrt{3}π}{2}$ | D. | $\frac{2\sqrt{2}π}{3}$ |
4.设a,b是非零实数,c∈R,若a<b,则下列不等式成立的是( )
| A. | a2<b2 | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ac<ac | D. | a-c<b-c |
5.已知i是虚数单位,若z1=2+i,z2=1-i,则$z=\frac{z_1}{z_2}$在复平面内的对应点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |