题目内容
4.已知函数f(x)=$\frac{(x-2)(x+a)}{x}$为奇函数,则a=2.分析 先求出函数的定义域,利用f(-1)=-f(1),即可得出结论.
解答 解:显然定义域为(-∞,0)∪(0,+∞).
由f(-1)=$\frac{-3(-1+a)}{-1}$=-(1-2)(1+a),
所以a=2.
故答案为:2.
点评 本题考查了利用函数的奇偶性定义,考查赋值法的运用,比较基础.

练习册系列答案
相关题目
14.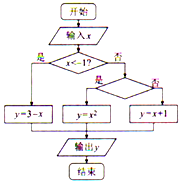 已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
 已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )| A. | x≥1? | B. | x≥-1? | C. | -1≤x≤2? | D. | x≤1? |
19.已知等比数列{an}的前n项和Sn=2n-1,则数列{an2}的前n项和Tn=( )
| A. | (2n-1)2 | B. | 4n-1 | C. | $\frac{{4}^{n}-1}{3}$ | D. | $\frac{{4}^{n+1}-4}{3}$ |
15.阅读下列程序框图,输出的结果s的值为( )
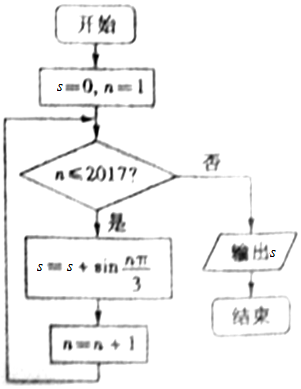

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |