题目内容

4．设a，b是非零实数，c∈R，若a＜b，则下列不等式成立的是（　　）
A．a2＜b2B．$\frac{1}{a}＞\frac{1}{b}$C．ac＜acD．a-c＜b-c

分析 利用不等式的基本性质即可得出

解答 解：若a=-2，b=1，则A不成立，
若a=-2，b-1，则B不成立，
若c=0，则C不成立，
根据不等式的性质可得a-c＜b-c成立，
故选：D

点评 本题考查了不等式的基本性质，属于基础题．

练习册系列答案
相关题目
13．摩拜单车和ofo小黄车等各种共享自行车已经遍布大街小巷，给我们的生活带来了便利．某自行车租车点的收费标准是：每车使用1小时之内是免费的，超过1小时的部分每小时收费2元（不足1小时的部分按1小时计算）．有甲、乙两人相互独立来该租车点租车（各租一车一次）．设甲、乙不超过两小时还车的概率分别为$\frac{1}{4}$，$\frac{1}{2}$；1小时以上且不超过2小时还车的概率分别为$\frac{1}{2}$，$\frac{1}{4}$；两人租车时间都不会超过3小时．
（Ⅰ）求甲乙两人所付的租车费用相同的概率；
（Ⅱ）设甲乙两人所付租车费用之和为随机变量ξ，求ξ的分布列与数学期望Eξ．
15．阅读下列程序框图，输出的结果s的值为（　　）
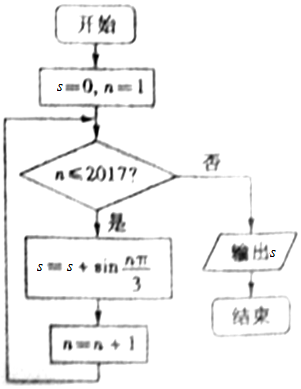
A．$\frac{{\sqrt{3}}}{2}$B．0C．$-\frac{{\sqrt{3}}}{2}$D．$\sqrt{3}$
12．（1）计算：sin$\frac{25π}{6}$+cos$\frac{25π}{3}$+tan（-$\frac{25π}{4}$）
（2）化简：$\frac{{sin（5π-α）cos（α+\frac{3}{2}π）cos（π+α）}}{{sin（α-\frac{3}{2}π）cos（α+\frac{π}{2}）tan（α-3π）}}$．
19．下列说法正确的是（　　）
A．三角形的内角是第一象限角或第二象限角
B．第一象限的角是锐角
C．第二象限的角比第一象限的角大
D．角α是第四象限角，则$2kπ-\frac{π}{2}＜α＜2kπ（k∈z）$
9．f（x）是R上的以3为周期的奇函数，且f（2）=0，则f（x）=0在[0，6]内解的个数为9．
16．若复数z满足$\frac{z+2i}{z}$=2+3i，其中i是虚数单位，则$\overline z$=（　　）
A．$\frac{2}{5}$+$\frac{3}{5}$iB．$\frac{3}{5}$+$\frac{2}{5}$iC．$\frac{3}{5}$+$\frac{1}{5}$iD．$\frac{3}{5}$-$\frac{1}{5}$i
13．设x∈R，且x≠0，若x+x-1=3，猜想${x^{2^n}}+{x^{-{2^n}}}（n∈{N^*}）$的个位数字是（　　）
A．5B．6C．7D．8
14．已知点N（x，y）为圆x2+y2=1上任意一点，则$\frac{y}{x+2}$的取值范围（　　）
A．[$-\frac{{\sqrt{3}}}{3}$，$\frac{{\sqrt{3}}}{3}$]B．[-$\sqrt{3}$，$\sqrt{3}$]C．（-∞，$-\frac{{\sqrt{3}}}{3}$]∪[$\frac{{\sqrt{3}}}{3}$，+∞）D．（-∞，-$\sqrt{3}$]∪[$\sqrt{3}$，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网