多项式(x2-2x-3)5展开式中含x项的系数为( )A．240B．-810C．480D．600 题目和参考答案——青夏教育精英家教网—

题目内容

3．多项式（x²-2x-3）⁵展开式中含x项的系数为（　　）

A．

240

B．

-810

C．

480

D．

600

分析将（x²-2x-3）⁵化为（x+1）⁵_^•（x-3）⁵，含x的项是由（x+1）⁵展开式中的常数项、x项与（x-3）⁵展开式中的_^x项、常数项分别对应相乘得到

解答解：将（x²-2x-3）⁵化为（x+1）⁵_^•（x-3）⁵，
含x的项是由（x+1）⁵展开式中的常数项、x项与（x-3）⁵展开式中的_^x项、常数项分别对应相乘得到．
（x+1）⁵展开式的通项为C₅^rx^5-r，常数项、^_x的项的系数分别为1，C₅⁴=5，
（x-3）⁵展开式的通项为C₅^kx^5-k（-3）^k，x项、常数项分别为C₅⁴（-3）⁴=405，-243
所以（x²-2x-3）⁵展开式中含x项的系数是405-243×5=-810
故选B．

点评本题考查二项式定理的应用，及转化、分类讨论、计算的能力．

练习册系列答案

13．摩拜单车和ofo小黄车等各种共享自行车已经遍布大街小巷，给我们的生活带来了便利．某自行车租车点的收费标准是：每车使用1小时之内是免费的，超过1小时的部分每小时收费2元（不足1小时的部分按1小时计算）．有甲、乙两人相互独立来该租车点租车（各租一车一次）．设甲、乙不超过两小时还车的概率分别为$\frac{1}{4}$，$\frac{1}{2}$；1小时以上且不超过2小时还车的概率分别为$\frac{1}{2}$，$\frac{1}{4}$；两人租车时间都不会超过3小时．
（Ⅰ）求甲乙两人所付的租车费用相同的概率；
（Ⅱ）设甲乙两人所付租车费用之和为随机变量ξ，求ξ的分布列与数学期望Eξ．

10．下列说法正确的是（　　）

	A．	命题“?x∈R，使得x²+x+1＜0”的否定是：“?x∈R，x²+x+1＞0”
	B．	命题“若x²-3x+2=0，则x=1或x=2”的否命题是：“若x²-3x+2=0，则x≠1或x≠2”
	C．	直线l₁：2ax+y+1=0，l₂：x+2ay+2=0，l₁∥l₂的充要条件是$a=\frac{1}{2}$
	D．	命题“若x=y，则sinx=siny”的逆否命题是真命题

17．已知等比数列{a_n}的前n项和为S_n，且$6{S_n}={3^{n+1}}+a$（a∈N₊）．
（Ⅰ）求a的值及数列{a_n}的通项公式；
（Ⅱ）设${b_n}=\frac{{{{（-1）}^{n-1}}（2{n^2}+2n+1）}}{{{{（{{log}_3}{a_n}+2）}^2}{{（{{log}_3}{a_n}+1）}^2}}}$，求{b_n}的前n项和T_n．

8．已知雨数f（x）=x²-x，g（x）=a1nx（a∈R），h（x）=kx+b（k，b∈R）．
（1）若函数F（x）=f（x）-g（x）在区间（0，1）上存在两个极值点，求实数a的取值范围；
（2）设a=1，记[x]表示不超过实数x的最大整数，如[1]=1，[1，2]=1，[-1，2]=-2，A={k|f（x）+x+1-h（x）][h（x）-2eg（x）]≥0对x＞0恒成立．若k₁，k₂∈A，求[k₂-k₁]的最大值数据是2（数据：ln2≈0.7．ln5=1.6）

15．阅读下列程序框图，输出的结果s的值为（　　）

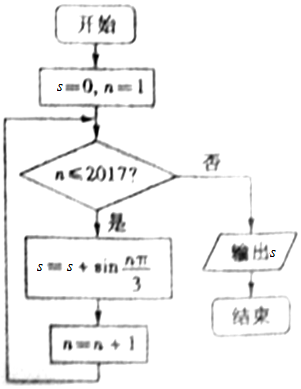
A．

$\frac{{\sqrt{3}}}{2}$

B．

C．

$-\frac{{\sqrt{3}}}{2}$

D．

$\sqrt{3}$

12．（1）计算：sin$\frac{25π}{6}$+cos$\frac{25π}{3}$+tan（-$\frac{25π}{4}$）
（2）化简：$\frac{{sin（5π-α）cos（α+\frac{3}{2}π）cos（π+α）}}{{sin（α-\frac{3}{2}π）cos（α+\frac{π}{2}）tan（α-3π）}}$．

13．设x∈R，且x≠0，若x+x^-1=3，猜想${x^{2^n}}+{x^{-{2^n}}}（n∈{N^*}）$的个位数字是（　　）

试题分类