题目内容
7.底面是边长为1的正方形,侧面是等边三角形的四棱锥的外接球的体积为( )| A. | $\frac{\sqrt{2}π}{3}$ | B. | $\frac{\sqrt{3}π}{3}$ | C. | $\frac{\sqrt{3}π}{2}$ | D. | $\frac{2\sqrt{2}π}{3}$ |
分析 画出图形,求出外接球的半径即可求出结果.
解答  解:底面ABCD外接圆的半径是$\frac{\sqrt{2}}{2}$,即AO=$\frac{\sqrt{2}}{2}$.
解:底面ABCD外接圆的半径是$\frac{\sqrt{2}}{2}$,即AO=$\frac{\sqrt{2}}{2}$.
则PO=$\sqrt{1-\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,
∴四棱锥的外接球的半径为:$\frac{\sqrt{2}}{2}$,
∴四棱锥的外接球的体积为$\frac{4}{3}π•(\frac{\sqrt{2}}{2})^{3}$=$\frac{\sqrt{2}π}{3}$.
故选:A.
点评 本题考查几何体的外接球的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
15.阅读下列程序框图,输出的结果s的值为( )
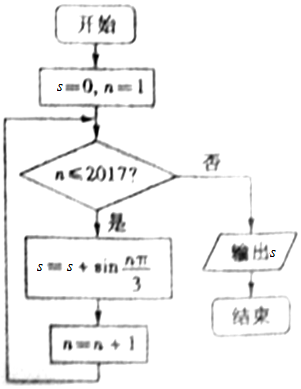

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{3}$ |
19.下列说法正确的是( )
| A. | 三角形的内角是第一象限角或第二象限角 | |
| B. | 第一象限的角是锐角 | |
| C. | 第二象限的角比第一象限的角大 | |
| D. | 角α是第四象限角,则$2kπ-\frac{π}{2}<α<2kπ(k∈z)$ |
16.若复数z满足$\frac{z+2i}{z}$=2+3i,其中i是虚数单位,则$\overline z$=( )
| A. | $\frac{2}{5}$+$\frac{3}{5}$i | B. | $\frac{3}{5}$+$\frac{2}{5}$i | C. | $\frac{3}{5}$+$\frac{1}{5}$i | D. | $\frac{3}{5}$-$\frac{1}{5}$i |