题目内容
5．已知i是虚数单位，若z1=2+i，z2=1-i，则$z=\frac{z_1}{z_2}$在复平面内的对应点位于（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 把z1=2+i，z2=1-i代入$z=\frac{z_1}{z_2}$，再由复数代数形式的乘除运算化简复数z，求出z在复平面内的对应点的坐标，则答案可求．
解答 解：由z1=2+i，z2=1-i，
得$z=\frac{z_1}{z_2}$=$\frac{2+i}{1-i}=\frac{（2+i）（1+i）}{（1-i）（1+i）}=\frac{1+3i}{2}=\frac{1}{2}+\frac{3}{2}i$，
则z在复平面内的对应点的坐标为：（$\frac{1}{2}$，$\frac{3}{2}$），位于第一象限．
故选：A．
点评 本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
相关题目
15．阅读下列程序框图，输出的结果s的值为（ ）
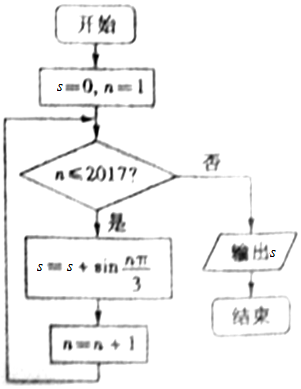
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | 0 | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\sqrt{3}$ |
16．若复数z满足$\frac{z+2i}{z}$=2+3i，其中i是虚数单位，则$\overline z$=（ ）
| A． | $\frac{2}{5}$+$\frac{3}{5}$i | B． | $\frac{3}{5}$+$\frac{2}{5}$i | C． | $\frac{3}{5}$+$\frac{1}{5}$i | D． | $\frac{3}{5}$-$\frac{1}{5}$i |
20．要得到函数y=sin（2x-$\frac{π}{4}$）的图象，只要将函数y=sin2x的图象（ ）
| A． | 向左平移$\frac{π}{4}$ | B． | 向右平移$\frac{π}{4}$ | C． | 向左平移$\frac{π}{8}$ | D． | 向右平移$\frac{π}{8}$ |
14．已知点N（x，y）为圆x2+y2=1上任意一点，则$\frac{y}{x+2}$的取值范围（ ）
| A． | [$-\frac{{\sqrt{3}}}{3}$，$\frac{{\sqrt{3}}}{3}$] | B． | [-$\sqrt{3}$，$\sqrt{3}$] | C． | （-∞，$-\frac{{\sqrt{3}}}{3}$]∪[$\frac{{\sqrt{3}}}{3}$，+∞） | D． | （-∞，-$\sqrt{3}$]∪[$\sqrt{3}$，+∞） |