题目内容

5．若复数（1+mi）（3+i）（i是虚数单位，m∈R）是纯虚数，则复数$\frac{m+3i}{1-i}$的模等于（　　）
A．1B．2C．3D．4

分析 由已知求得m，代入$\frac{m+3i}{1-i}$，利用复数代数形式的乘除运算化简，再由复数模的计算公式求解．

解答 解：∵（1+mi）（3+i）=3-m+（3m+1）i为纯虚数，
∴m=3，
则$\frac{m+3i}{1-i}$=$\frac{3+3i}{1-i}=\frac{3（1+i）^{2}}{（1-i）（1+i）}=3i$，
∴复数$\frac{m+3i}{1-i}$的模等于3．
故选：C．

点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，考查复数模的求法，是基础题．

练习册系列答案
相关题目
15．己知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点分别为F1（-c，0）和F2（c，0）（c＞0），A、C是椭圆短轴的两端点，过点E（3c，0）的直线AE与椭圆相交于另一点B，且F1A∥F2B
（I ）求椭圆的离心率；
（II）设直线F2B上有一点H（m，n）（m≠0）在△AF1C的外接圆上，求$\frac{n}{m}$的值．
16．设i为虚数单位，复数z满足z（2-i）=i3，则复数z的虚部为$-\frac{2}{5}$．
13．摩拜单车和ofo小黄车等各种共享自行车已经遍布大街小巷，给我们的生活带来了便利．某自行车租车点的收费标准是：每车使用1小时之内是免费的，超过1小时的部分每小时收费2元（不足1小时的部分按1小时计算）．有甲、乙两人相互独立来该租车点租车（各租一车一次）．设甲、乙不超过两小时还车的概率分别为$\frac{1}{4}$，$\frac{1}{2}$；1小时以上且不超过2小时还车的概率分别为$\frac{1}{2}$，$\frac{1}{4}$；两人租车时间都不会超过3小时．
（Ⅰ）求甲乙两人所付的租车费用相同的概率；
（Ⅱ）设甲乙两人所付租车费用之和为随机变量ξ，求ξ的分布列与数学期望Eξ．
20．已知直线C1：$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$（t为参数），C2：$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数），当α=$\frac{π}{3}$时，则C1与C2的交点坐标为（1，0），（$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$）．
10．下列说法正确的是（　　）
A．命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，x2+x+1＞0”
B．命题“若x2-3x+2=0，则x=1或x=2”的否命题是：“若x2-3x+2=0，则x≠1或x≠2”
C．直线l1：2ax+y+1=0，l2：x+2ay+2=0，l1∥l2的充要条件是$a=\frac{1}{2}$
D．命题“若x=y，则sinx=siny”的逆否命题是真命题
17．已知等比数列{an}的前n项和为Sn，且$6{S_n}={3^{n+1}}+a$（a∈N+）．
（Ⅰ）求a的值及数列{an}的通项公式；
（Ⅱ）设${b_n}=\frac{{{{（-1）}^{n-1}}（2{n^2}+2n+1）}}{{{{（{{log}_3}{a_n}+2）}^2}{{（{{log}_3}{a_n}+1）}^2}}}$，求{bn}的前n项和Tn．
15．阅读下列程序框图，输出的结果s的值为（　　）
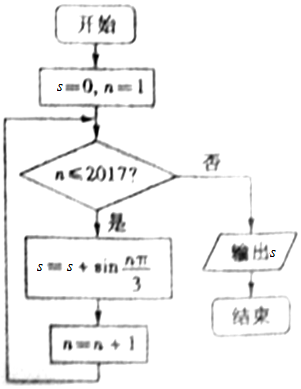
A．$\frac{{\sqrt{3}}}{2}$B．0C．$-\frac{{\sqrt{3}}}{2}$D．$\sqrt{3}$
16．若复数z满足$\frac{z+2i}{z}$=2+3i，其中i是虚数单位，则$\overline z$=（　　）
A．$\frac{2}{5}$+$\frac{3}{5}$iB．$\frac{3}{5}$+$\frac{2}{5}$iC．$\frac{3}{5}$+$\frac{1}{5}$iD．$\frac{3}{5}$-$\frac{1}{5}$i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网