题目内容
4.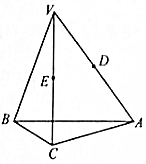 如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.
如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.(1)当DE⊥平面VBC时,判断直线DE与平面ABC的位置关系,并说明理由;
(2)当D、E分别为线段VA、VC上的中点,且BC=1,CA=$\sqrt{3}$,VC=2时,求三棱锥A-BDE的体积.
分析 (1)当DE⊥平面VBC时,DE⊥VC,推导出VC⊥AC,从而DE∥AC,由此能证明直线DE∥平面ABC.
(2)三棱锥A-BDE的体积为VA-BDE=VB-ADE,由此能求出三棱锥A-BDE的体积.
解答 解:(1)直线DE∥平面ABC.
证明如下:
∵VC?平面VBC,∴当DE⊥平面VBC,DE⊥VC,
∵AC?平面ABC,VC⊥平面ABC,∴VC⊥AC,
∵VC,DE,AC?平面VAC,∴DE∥AC,
∵AC?平面ABC,DE?平面ABC,
∴直线DE∥平面ABC.
(2)VC⊥平面ABC,∴VC⊥BC,
又BC⊥AC,在平面VAC内,VC∩AC=C,∴BC⊥平面VCA,
∴三棱锥A-BDE的体积为VA-BDE=VB-ADE=$\frac{1}{3}BC•{S}_{△ADE}$,
∵D,E分别是VA,VC上的中点,∴DE∥AC,且DE=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$,
∴DE⊥VC,S△ADE=S△CDE=$\frac{1}{2}DE•CE$=$\frac{\sqrt{3}}{4}$,
∴三棱锥A-BDE的体积VA-BDE=VB-ADE=$\frac{1}{3}BC•{S}_{△ADE}$=$\frac{1}{3}×\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{12}$.
点评 本题考查线面位置关系的判断与证明,考查柱、锥、台体的体积,考查空间想象能力与计算能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.某几何体的三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是( )
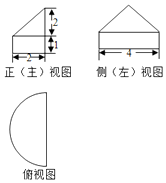

| A. | 3π | B. | $\frac{10π}{3}$ | C. | $\frac{11π}{3}$ | D. | 4π |
19.已知等差数列{an}的前n项和为Sn,若S10=55,则a3+a8=( )
| A. | 5 | B. | $\frac{11}{2}$ | C. | 10 | D. | 11 |
9.已知P(x,y)(其中x≠0)为双曲线$\frac{{y}^{2}}{4}$-x2=1上任一点,过P点向双曲线的两条渐近线分别作垂线,垂足分别为A、B,则△PAB的面积为( )
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{8}{25}$ | D. | 与点P的位置有关 |
16.如图所示的程序框图中,输出的S的值是( )
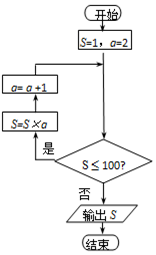

| A. | 80 | B. | 100 | C. | 120 | D. | 140 |