已知等差数列{an}的前n项和为Sn.若S10=55.则a3+a8=( )A．5B．$\frac{11}{2}$C．10D．11 题目和参考答案——青夏教育精英家教网——

题目内容

19．已知等差数列{a_n}的前n项和为S_n，若S₁₀=55，则a₃+a₈=（　　）

A．

5

B．

$\frac{11}{2}$

C．

10

D．

11

分析利用等差数列前n项和公式得到S₁₀=5（a₃+a₈），由此能求出a₃+a₈的值．

解答解：∵等差数列{a_n}的前n项和为S_n，S₁₀=55，
∴S₁₀=$\frac{10}{2}（{a}_{1}+{a}_{10}）$=$\frac{10}{2}（{a}_{3}+{a}_{8}）$=5（a₃+a₈）=55，
解得a₃+a₈=11．
故选：D．

点评本题考查了等差数列的通项公式，考查了等差数列的前n项和，是基础题．

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

初中英语听力与阅读系列答案

领航英语阅读理解与完形填空系列答案

英语拓展听力与阅读系列答案

阅读组合突破系列答案

初中英语阅读系列答案

全程探究阅读系列答案

相关题目

9．已知A（1，2），B（2，11），若直线y=（m-$\frac{6}{m}$）x+1（m≠0）与线段AB相交，则实数m的取值范围是（　　）

[-2，0）∪[3，+∞）

（-∞，-1]∪（0，6]

[-2，-1]∪[3，6]

[-2，0）∪（0，6]

10．设椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{8-{a}^{2}}$=1（a＞0）的焦点在x轴上．
（Ⅰ）若椭圆E的离心率e=$\frac{\sqrt{2}}{5}$a，求椭圆E的方程；
（Ⅱ）设F₁、F₂分别是椭圆E的左、右焦点，P为直线x+y=2$\sqrt{2}$与椭圆E的一个公共点，直线F₂P交y轴于点Q，连结F₁P，问当a变化时，$\overrightarrow{{F}_{1}P}$与$\overrightarrow{{F}_{1}Q}$的夹角是否为定值，若是定值，求出该定值，若不是定值，说明理由．

7．已知圆C₁：x²+y²=r²（r＞0）与抛物线C₂：x²=2py（p＞0），点（$\sqrt{2}$，-2）是圆C₁与抛物线C₂准线l的一个交点．
（1）求圆C₁与抛物线C₂的方程；
（2）若点M是直线l上的动点，过点M作抛物线C₂的两条切线，切点分别为A、B，直线AB与圆C₁交于点E、F，求$\overrightarrow{OE}$•$\overrightarrow{OF}$的取值范围．

14．某大学有甲、乙两个图书馆，对其借书、还书的等待时间进行调查，得到下表：
甲图书馆

借（还）书等待时间T₁（分钟）	1	2	3	4	5
频数	1500	1000	500	500	1500

借（还）书等待时间T₂（分钟）	1	2	3	4	5
频数	1000	500	2000	1250	250

以表中等待时间的学生人数的频率为概率．
（1）分别求在甲、乙两图书馆借书的平均等待时间；
（2）学校规定借书、还书必须在同一图书馆，某学生需要借一本数学参考书，并希望借、还书的等待时间之和不超过4分钟，在哪个图书馆借、还书更能满足他的要求？

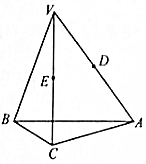如图所示，在Rt△ABC中，AC⊥BC，过点C的直线VC垂直于平面ABC，D、E分别为线段VA、VC上异于端点的点．
（1）当DE⊥平面VBC时，判断直线DE与平面ABC的位置关系，并说明理由；
（2）当D、E分别为线段VA、VC上的中点，且BC=1，CA=$\sqrt{3}$，VC=2时，求三棱锥A-BDE的体积．

11．已知双曲线C₂与椭圆C₁：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1具有相同的焦点，则两条曲线相交四个交点形成四边形面积最大时双曲线C₂的离心率为$\sqrt{2}$．

6．一个均匀小正方体的6个面中，三个面上标以数字0，两个面上标以数字1，一个面上标以数字2，将这个小正方体抛掷1次，则向上的数字为2的概率为$\frac{1}{6}$；将这个小正方体抛掷2次，则向上的数字之积的数学期望是$\frac{4}{9}$．

7．已知直线y=ax-2与直线y=（a+2）x-2互相垂直，则a=（　　）