题目内容
9.已知P(x,y)(其中x≠0)为双曲线$\frac{{y}^{2}}{4}$-x2=1上任一点,过P点向双曲线的两条渐近线分别作垂线,垂足分别为A、B,则△PAB的面积为( )| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{8}{25}$ | D. | 与点P的位置有关 |
分析 由题意,O,P,A,B四点共圆,∠APB=∠AOB,tan$\frac{1}{2}∠AOB$=2,sin∠AOB=$\frac{4}{5}$,求出|PA||PB|,即可得出结论.
解答  解:由题意,O,P,A,B四点共圆,∠APB=∠AOB,tan$\frac{1}{2}∠AOB$=2,sin∠AOB=$\frac{4}{5}$,
解:由题意,O,P,A,B四点共圆,∠APB=∠AOB,tan$\frac{1}{2}∠AOB$=2,sin∠AOB=$\frac{4}{5}$,
设P(x,y),双曲线的渐近线方程为y=±2x,则|PA||PB|=$\frac{|2x+y|}{\sqrt{5}}•\frac{|2x-y|}{\sqrt{5}}$=$\frac{4}{5}$,
∴△PAB的面积为$\frac{1}{2}•$$\frac{4}{5}$•$\frac{4}{5}$=$\frac{8}{25}$.
故选C.
点评 本题考查双曲线的性质,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.已知棱长均为1的四棱锥顶点都在球O1的表面上,棱长均为2的四面体顶点都在球O2的表面上,若O1、O2的表面积分别是S1、S2,则S1:S2=( )
| A. | 2:3 | B. | 1:3 | C. | 1:4 | D. | 1:$\sqrt{3}$ |
17.已知i为虚数单位,则复数$\frac{1+i}{2i}$=( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
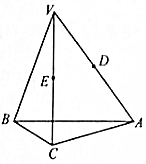 如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.
如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.