题目内容
12.已知△ABC的三个顶点分别为A(1,2),B(-3,4),C(2,-6),求:(1)边BC的垂直平分线的方程;
(2)AC边上的中线BD所在的直线方程.
分析 (1)利用中点坐标公式、和斜率公式,利用斜截式即可得出.
(2)利用中点坐标公式和两点式的关系即可得出.
解答 解:(1)∵A(1,2),B(-3,4),C(2,-6),
∴kBC=$\frac{-6-4}{2+3}$=-2,
∴边BC的垂直平分线的方程的斜率为$\frac{1}{2}$,BC边的中点的坐标为($\frac{-3+2}{2}$,$\frac{4-6}{2}$),即为(-$\frac{1}{2}$,-1),
∴边BC的垂直平分线的方程为y+1=$\frac{1}{2}$(x+$\frac{1}{2}$),即为2x-4y-3=0,
(2)AC边上的中点D的坐标为($\frac{1+2}{2}$,$\frac{2-6}{2}$),即为($\frac{3}{2}$,-2),
∴AC边上的中线BD所在的直线方程为$\frac{y-4}{-2-4}$=$\frac{x+3}{\frac{3}{2}+3}$,即为4x+3y=0.
点评 本题考查了中点坐标公式、两点式、两条直线垂直与斜率之间的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
7.已知直线y=ax-2与直线y=(a+2)x-2互相垂直,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
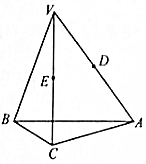 如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.
如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.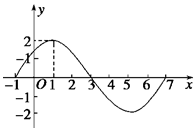 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.