某几何体的三视图如图所示.其俯视图是由一个半圆与其直径组成的图形.则此几何体的体积是( )A．3πB．$\frac{10π}{3}$C．$\frac{11π}{3}$D．4π 题目和参考答案——青夏教育精英家教网—

题目内容

14．某几何体的三视图如图所示，其俯视图是由一个半圆与其直径组成的图形，则此几何体的体积是（　　）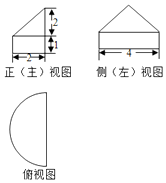

A．

3π

B．

$\frac{10π}{3}$

C．

$\frac{11π}{3}$

D．

4π

分析根据三视图可知几何体是组合体：上面是半个圆锥、下面是半个圆柱，并求出底面圆的半径以及几何体的高，由椎体、柱体的体积公式求出此几何体的体积．

解答解：根据三视图可知几何体是组合体：上面是半个圆锥、下面是半个圆柱，
且圆锥的底面圆的半径r=2、高是2，圆柱的底面圆的半径r=2、高是1，
所以此几何体的体积V=$\frac{1}{2}×\frac{1}{3}π×4×2+\frac{1}{2}π×4×1$=$\frac{10π}{3}$，
故选B．

点评本题考查三视图求几何体的体积，由三视图正确复原几何体是解题的关键，考查空间想象能力．

练习册系列答案

5．设|a|＜1，函数f（x）=ax²+x-a（-1≤x≤1），证明：|f（x）|≤$\frac{5}{4}$．

2．已知锐角三角形ABC中，角A，B，C所对的边分别为a，b，c若c-a=2acosB，则$\frac{si{n}^{2}A}{sin（B-A）}$的取值范围是（$\frac{1}{2}$，$\frac{\sqrt{2}}{2}$）．

9．已知A（1，2），B（2，11），若直线y=（m-$\frac{6}{m}$）x+1（m≠0）与线段AB相交，则实数m的取值范围是（　　）

19．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率$e=\frac{{\sqrt{6}}}{3}$，直线y=bx+2与圆x²+y²=2相切．
（1）求椭圆的方程；
（2）已知定点E（1，0），若直线y=kx+2（k≠0）与椭圆相交于C，D两点，试判断是否存在实数k，使得以CD为直径的圆过定点E？若存在，求出k的值；若不存在，请说明理由．

6．已知函数$f（x）=\left\{\begin{array}{l}-sinx，x＞0\\ sinx，x≤0\end{array}\right.$，则下列结论正确的是（　　）

	A．	f（x）是奇函数
	B．	f（x）是偶函数
	C．	f（x）是周期函数
	D．	f（x）在$[-\frac{π}{2}+2kπ，\frac{π}{2}+2kπ]（k∈z）$上为减函数

3．

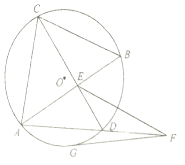如图所示，E是园O内两条弦AB和CD的交点，过AD延长线上一点F作圆O的切线FG，G为切点，已知EF=FG．求证：EF∥CB．

4．

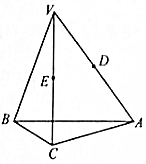如图所示，在Rt△ABC中，AC⊥BC，过点C的直线VC垂直于平面ABC，D、E分别为线段VA、VC上异于端点的点．
（1）当DE⊥平面VBC时，判断直线DE与平面ABC的位置关系，并说明理由；
（2）当D、E分别为线段VA、VC上的中点，且BC=1，CA=$\sqrt{3}$，VC=2时，求三棱锥A-BDE的体积．

试题分类