题目内容
11.已知O是平面上一定点,A,B,C是平面上不共线的三个点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ(${\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|cosC}}}$),λ∈(0,+∞),则动点P的轨迹一定通过△ABC的( )| A. | 重心 | B. | 垂心 | C. | 外心 | D. | 内心 |
分析 可先根据数量积为零得出 $\overrightarrow{BC}$与λ(${\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|cosC}}}$),垂直,可得点P在BC的高线上,从而得到结论.
解答 解:由$\overrightarrow{OP}$=$\overrightarrow{OA}$+λ(${\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|cosC}}}$)⇒$\overrightarrow{OP}$-$\overrightarrow{OA}$=λ(${\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|cosC}}}$)⇒,$\overrightarrow{AP}$=λ(${\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|cosC}}}$),
又∵$\overrightarrow{BC}•$$\overrightarrow{AP}$=λ(${\frac{{\overrightarrow{AB}}}{{|{\overrightarrow{AB}}|cosB}}$+$\frac{{\overrightarrow{AC}}}{{|{\overrightarrow{AC}}|cosC}}}$)$•\overrightarrow{BC}$=-|$\overrightarrow{BC}$|+|$\overrightarrow{BC}$|=0,∴$\overrightarrow{AP}⊥\overrightarrow{BC}$
∴点P在BC的高线上,即P的轨迹过△ABC的垂心
故选B.
点评 本题主要考查了向量在几何中的应用、空间向量的加减法、轨迹方程、以及三角形的五心等知识,属于中档题.

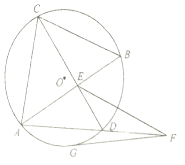 如图所示,E是园O内两条弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证:EF∥CB.
如图所示,E是园O内两条弦AB和CD的交点,过AD延长线上一点F作圆O的切线FG,G为切点,已知EF=FG.求证:EF∥CB.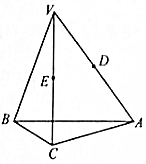 如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.
如图所示,在Rt△ABC中,AC⊥BC,过点C的直线VC垂直于平面ABC,D、E分别为线段VA、VC上异于端点的点.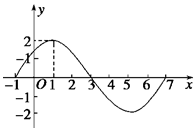 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<$\frac{π}{2}$,x∈R)的图象的一部分如图所示.