题目内容
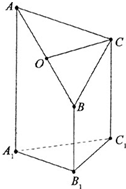 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.(1)证明:OC∥平面A1B1C1;
(2)求异面直线OC与AlBl所成角的正切值.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)由题意及图形,利用直三棱柱的特点,因为O为中点连接OD,由题意利用借助线面垂直的判定定理证明OC∥平面A1B1C1;
(2)取AlB的中点M,则OC∥MC1,∠C1MB1为异面直线OC与AlBl所成角,可求异面直线OC与AlBl所成角的正切值.
(2)取AlB的中点M,则OC∥MC1,∠C1MB1为异面直线OC与AlBl所成角,可求异面直线OC与AlBl所成角的正切值.
解答:
(1)证明:作OD∥AA1交A1B1于D,连C1D.
则OD∥BB1∥CC1.
因为O是AB的中点,
所以OD=
(AA1+BB1)=3=CC1.
则ODC1C是平行四边形,因此有OC∥C1D.C1D?平面C1B1A1且OC?平面C1B1A1,
则OC∥面A1B1C1.
(2)解:取AlB的中点M,则OC∥MC1,
∴∠C1MB1为异面直线OC与AlBl所成角,
∴异面直线OC与AlBl所成角的正切值为2.
则OD∥BB1∥CC1.
因为O是AB的中点,
所以OD=
| 1 |
| 2 |
则ODC1C是平行四边形,因此有OC∥C1D.C1D?平面C1B1A1且OC?平面C1B1A1,
则OC∥面A1B1C1.
(2)解:取AlB的中点M,则OC∥MC1,
∴∠C1MB1为异面直线OC与AlBl所成角,
∴异面直线OC与AlBl所成角的正切值为2.
点评:此题重点考查了线面平行的判定定理,考查异面直线OC与AlBl所成角的正切值,属于中档题.

练习册系列答案
相关题目
已知A,B,C三点共线,且直线AB不过点O,
=m
+n
,则m2+n的最小值为( )
| OC |
| OA |
| OB |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
下列说法中正确的是( )
| A、数列{lg2n}是等差数列而不是等比数列 |
| B、公比q>1的等比数列中各项都大于1 |
| C、公比q<0的等比数列是递减数列 |
| D、常数列是公比为1的等比数列 |
 如图,已知三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,PC=BC=4,AB=2,E、F分别是PB、PA的中点.
如图,已知三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,PC=BC=4,AB=2,E、F分别是PB、PA的中点.