题目内容
已知椭圆
+
=1(a>b>0)的离心率为
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
+1).一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点.
(1)求椭圆和双曲线的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2,证明:k1•k2=1.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(1)求椭圆和双曲线的标准方程;
(2)设直线PF1、PF2的斜率分别为k1、k2,证明:k1•k2=1.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由题意知,确定椭圆离心率,利用椭圆的定义得到又2a+2c=4(
+1),解方程组即可求得椭圆的方程,等轴双曲线的顶点是该椭圆的焦点可求得该双曲线的方程;
(2)设点P(x0,y0),根据斜率公式求得k1、k2,把点P(x0,y0)在双曲线上,即可证明结果.
| 2 |
(2)设点P(x0,y0),根据斜率公式求得k1、k2,把点P(x0,y0)在双曲线上,即可证明结果.
解答:
解:(1)设椭圆的半焦距为c,由题意知:
=
,2a+2c=4(
+1),
所以a=2
,c=2,
又a2=b2+c2,因此b=2.
故椭圆的标准方程为
+
=1.(4分)
由题意设等轴双曲线的标准方程为
-
=1(m>0),
因为等轴双曲线的顶点是椭圆的焦点,所以m=2,
因此双曲线的标准方程为
-
=1.(8分)
(2)证明:P(x0,y0),
则k1=
,k2=
.
因为点P在双曲线x2-y2=4上,所以x02-y02=4.
因此k1k2=
•
=1.,即k1k2=1.(14分)
| c |
| a |
| ||
| 2 |
| 2 |
所以a=2
| 2 |
又a2=b2+c2,因此b=2.
故椭圆的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
由题意设等轴双曲线的标准方程为
| x2 |
| m2 |
| y2 |
| m2 |
因为等轴双曲线的顶点是椭圆的焦点,所以m=2,
因此双曲线的标准方程为
| x2 |
| 4 |
| y2 |
| 4 |
(2)证明:P(x0,y0),
则k1=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
因为点P在双曲线x2-y2=4上,所以x02-y02=4.
因此k1k2=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
点评:本题考查了椭圆的定义、离心率、椭圆与双曲线的标准方程、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
从5名男生和3名女生中选出3名志愿者,其中男生和女生都至少有1人被选中,则不同的选法方案共有( )
| A、45种 | B、10种 |
| C、9种 | D、46种 |
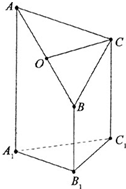 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.