题目内容
等比数列an中的前三项a1,a2,a3分别是下面数阵中第一、二、三行中的某三个数,且三个数不在同一列.
(1)求此数列{an}的通项公式;
(2)若数列{bn}满足bn=3an-(-1)nlgan,求数列{bn}的前n项和Sn.
|
(1)求此数列{an}的通项公式;
(2)若数列{bn}满足bn=3an-(-1)nlgan,求数列{bn}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知得a1=3,a2=6,a3=12,公比q=2,由此能求出数列{an}的通项公式.
(2)由an=3•2n-1,得bn=3an-(-1)nlgan=9×2n-1-(-1)n[lg3+(n-1)lg2],由此能求出数列{bn}的前n项和Sn.
(2)由an=3•2n-1,得bn=3an-(-1)nlgan=9×2n-1-(-1)n[lg3+(n-1)lg2],由此能求出数列{bn}的前n项和Sn.
解答:
解:(1)经检验,当a1=5或a1=4时,不可能得到符合题意的等比数列,
∴a1=3,a2=6,a3=12,公比q=2,
∴an=3•2n-1.
(2)由an=3•2n-1,得bn=3an-(-1)nlgan=9×2n-1-(-1)n[lg3+(n-1)lg2],
∴Sn=9(1+2+…+2n-1)-[(-1)+(-1)2+…+(-1)n](lg3-lg2),
n为偶数时,Sn=9×
+(lg3-lg2)-(
-n)lg2=9(2n-1)+
lg2+lg3.
n为奇数时,Sn=9×
+(lg3-lg2)-(
-n)lg2=9(2n-1)+
lg2+lg3.
∴Sn=
.
∴a1=3,a2=6,a3=12,公比q=2,
∴an=3•2n-1.
(2)由an=3•2n-1,得bn=3an-(-1)nlgan=9×2n-1-(-1)n[lg3+(n-1)lg2],
∴Sn=9(1+2+…+2n-1)-[(-1)+(-1)2+…+(-1)n](lg3-lg2),
n为偶数时,Sn=9×
| 1-2n |
| 1-2 |
| n-1 |
| 2 |
| n-1 |
| 2 |
n为奇数时,Sn=9×
| 1-2n |
| 1-2 |
| n-1 |
| 2 |
| n-1 |
| 2 |
∴Sn=
|
点评:本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要注意分类讨论思想的合理运用.

练习册系列答案
相关题目
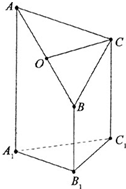 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.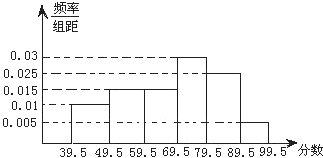 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图:观察图形,回答下列问题: