题目内容
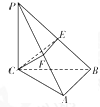如图，已知三棱锥P-ABC中，PC⊥平面ABC，AB⊥BC，PC=BC=4，AB=2，E、F分别是PB、PA的中点．（1）求证：侧面PAB⊥侧面PBC；
（2）求三棱锥P-CEF的外接球的表面积．
考点：平面与平面垂直的判定,球内接多面体
专题：空间位置关系与距离
分析：（1）由已知得AB⊥PC，AB⊥BC，从而AB⊥侧面PBC，由此能证明侧面PAB⊥侧面PBC．
（2）由已知得CE⊥PB，CE⊥EF．从而EF⊥侧面PBC，故EC、EF、EP两两垂直，从而三棱锥P-CEF的外接球就是以EC、EF、EP为长、宽、高的长方体的外接球，由此能求出三棱锥P-CEF的外接球的表面积．
（2）由已知得CE⊥PB，CE⊥EF．从而EF⊥侧面PBC，故EC、EF、EP两两垂直，从而三棱锥P-CEF的外接球就是以EC、EF、EP为长、宽、高的长方体的外接球，由此能求出三棱锥P-CEF的外接球的表面积．
解答：
（1）证明：∵PC⊥平面ABC，∴AB⊥PC，
又AB⊥BC，则AB⊥侧面PBC，AB?侧面PAB，
故侧面PAB⊥侧面PBC．（6分）
（2）解：∵PC=BC=4，E为PB的中点，∴CE⊥PB，
而侧面PAB垂直侧面PBC于PB，∴CE⊥EF．
由E、F分别是PB、PA的中点有EF∥AB，
则EF⊥侧面PBC．
故EC、EF、EP两两垂直，（9分）
三棱锥P-CEF的外接球就是以EC、EF、EP为长、宽、高的长方体的外接球，
由已知得EC=EP=2
，EF=1，
其外接球的直径是
=
，
故所求三棱锥P-CEF的外接球的表面积是=17π．（12分）
又AB⊥BC，则AB⊥侧面PBC，AB?侧面PAB，
故侧面PAB⊥侧面PBC．（6分）
（2）解：∵PC=BC=4，E为PB的中点，∴CE⊥PB，
而侧面PAB垂直侧面PBC于PB，∴CE⊥EF．
由E、F分别是PB、PA的中点有EF∥AB，
则EF⊥侧面PBC．
故EC、EF、EP两两垂直，（9分）
三棱锥P-CEF的外接球就是以EC、EF、EP为长、宽、高的长方体的外接球，
由已知得EC=EP=2
| 2 |
其外接球的直径是
| 8+8+1 |
| 17 |
故所求三棱锥P-CEF的外接球的表面积是=17π．（12分）
点评：本题考查侧面PAB⊥侧面PBC的证明，考查三棱锥P-CEF的外接球的表面积的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阶梯计算系列答案
相关题目
若a，b都是实数，则“a-b＞0”是“a2-b2＞0”的（ ）
| A、既不充分也不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、充分而不必要条件 |
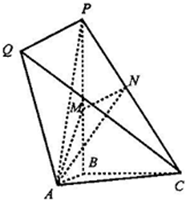如图所示的几何体中，PB⊥面ABC，PQ∥AB，PQ=PB=1；Rt△ABC中，∠ABC=90°，AB=BC=
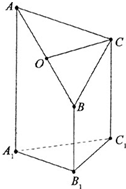如图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=B1C1=l，∠AlBlC1=90°，AAl=4，BBl=2，CCl=3，且设点O是AB的中点．