题目内容
下列说法中正确的是（ ）
| A、数列{lg2n}是等差数列而不是等比数列 |
| B、公比q＞1的等比数列中各项都大于1 |
| C、公比q＜0的等比数列是递减数列 |
| D、常数列是公比为1的等比数列 |
考点：等比数列的通项公式
专题：等差数列与等比数列
分析：利用等比数列和等差数列的性质求解．
解答：
解：∵lg2n=nlg2，
∴lg2n+1-lg2n=lg2，
=
不是常数，
∴数列{lg2n}是等差数列而不是等比数列，故A正确；
公比q＞1的等比数列中各项都同号，故B错误；
公比q＜0的等比数列中相邻两项异号，故C错误；
常数列是公比为1的等比数列或各项都是0的数列，故D错误．
故选：A．
∴lg2n+1-lg2n=lg2，
| lg2n+1 |
| lg2n |
| n+1 |
| n |
∴数列{lg2n}是等差数列而不是等比数列，故A正确；
公比q＞1的等比数列中各项都同号，故B错误；
公比q＜0的等比数列中相邻两项异号，故C错误；
常数列是公比为1的等比数列或各项都是0的数列，故D错误．
故选：A．
点评：本题考查命题真假的判断，是基础题，解题时要注意等比数列和等差数列的性质的合理运用．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
用秦九韶算法计算函数f（x）=x6-x5-2x4+3x3+5x-4，当x=-2时的函数值是（ ）
| A、25 | B、62 | C、23 | D、26 |
“直线a，b是异面直线”是“直线a，b无公共点”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也必要条件 |
从5名男生和3名女生中选出3名志愿者，其中男生和女生都至少有1人被选中，则不同的选法方案共有（ ）
| A、45种 | B、10种 |
| C、9种 | D、46种 |
二次函数f（x）的二次项系数为正数，且对任意x∈R都有f（x）=f（4-x）成立，若f（2-a2）＜f（1+a-a2），那么a的取值范围是（ ）
| A、1＜a＜2 | B、a＞1 |
| C、a＞2 | D、a＜1 |
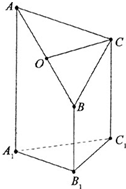如图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=B1C1=l，∠AlBlC1=90°，AAl=4，BBl=2，CCl=3，且设点O是AB的中点．