题目内容
设i是虚数单位,复数z=
.
(Ⅰ)若z=
,求实数k的值;
(Ⅱ)若z为纯虚数,求复数z.
| 1+ki |
| 2-i |
(Ⅰ)若z=
| 1 |
| 2 |
(Ⅱ)若z为纯虚数,求复数z.
考点:复数的基本概念
专题:数系的扩充和复数
分析:根据复数的有关概念建立条件关系即可得到结论.
解答:
解:(Ⅰ)由z=
得
=
,…(2分)
从而1+ki=
(2-i)=1-
,…(4分)
根据复数相等可知k=-
. …(6分)
(Ⅱ)z=
=
=
+
i,…(8分)
若z为纯虚数,则
…(10分)
解得k=2,从而z=i.…(12分)
| 1 |
| 2 |
| 1+ki |
| 2-i |
| 1 |
| 2 |
从而1+ki=
| 1 |
| 2 |
| i |
| 2 |
根据复数相等可知k=-
| 1 |
| 2 |
(Ⅱ)z=
| 1+ki |
| 2-i |
| (1+ki)(2+i) |
| (2-i)(2+i) |
| 2-k |
| 5 |
| 2k+1 |
| 5 |
若z为纯虚数,则
|
解得k=2,从而z=i.…(12分)
点评:本题主要考查复数的有关概念的应用,比较基础.

练习册系列答案
相关题目
设全集U=R,集合A={x|x
≤-1}和B={y|y=lg(x2+1)},则(∁UA)∩B=( )
| 1 |
| 3 |
| A、{x|x≤-1或x≥0} |
| B、{(x,y)|x≤-1,y≥0} |
| C、{x|x≥0} |
| D、{x|x>-1} |
从5名男生和3名女生中选出3名志愿者,其中男生和女生都至少有1人被选中,则不同的选法方案共有( )
| A、45种 | B、10种 |
| C、9种 | D、46种 |
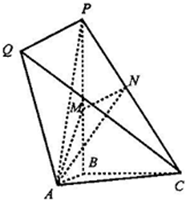 如图所示的几何体中,PB⊥面ABC,PQ∥AB,PQ=PB=1;Rt△ABC中,∠ABC=90°,AB=BC=
如图所示的几何体中,PB⊥面ABC,PQ∥AB,PQ=PB=1;Rt△ABC中,∠ABC=90°,AB=BC=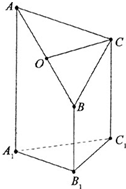 如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.
如图是一个直三棱柱(以A1B1C1为底面)被一平面所截得到的几何体,截面为ABC.已知A1B1=B1C1=l,∠AlBlC1=90°,AAl=4,BBl=2,CCl=3,且设点O是AB的中点.