题目内容
 数列{an}满足an+1=
数列{an}满足an+1=| 1 |
| 2-an |
(Ⅰ)计算a2、a3、a4,并推测an的表达式;
(Ⅱ)请用数学归纳法证明你在(Ⅰ)中的猜想.
考点:数学归纳法,归纳推理
专题:点列、递归数列与数学归纳法
分析:本题先根据题目中递推关系式,由a1=0,求出a2、a3、a4,并推测an的表达式,然后用数学归纳法加以证明,得到本题结论.
解答:
解:( I) a2=
=
; a3=
=
; a4=
=
,
由此猜想an=
(n∈N*);
( II)证明:(数学归纳法)
①当n=1时,a1=0,结论成立,
②假设n=k(k≥1,且k∈N*)时结论成立,
即ak=
,
当n=k+1时,ak+1=
=
=
,
∴当n=k+1时结论成立,
由①②知:对于任意的n∈N*,a n=
恒成立.
| 1 |
| 2-a1 |
| 1 |
| 2 |
| 1 |
| 2-a2 |
| 2 |
| 3 |
| 1 |
| 2-a3 |
| 3 |
| 4 |
由此猜想an=
| n+1 |
| n |
( II)证明:(数学归纳法)
①当n=1时,a1=0,结论成立,
②假设n=k(k≥1,且k∈N*)时结论成立,
即ak=
| k-1 |
| k |
当n=k+1时,ak+1=
| 1 |
| 2-ak |
| 1 | ||
2-
|
| (k+1)-1 |
| k+1 |
∴当n=k+1时结论成立,
由①②知:对于任意的n∈N*,a n=
| n-1 |
| n |
点评:本题考查了数学归纳法,通过猜想再证明的方法求数列的通项,本题难度不大,属于基础题.

练习册系列答案
相关题目
集合M={(x,y)|x=
},N={(x,y)|y=x+m},若M∩N的子集恰有4个,则M的取值范围是( )
| 1-y2 |
A、[-
| ||||
B、[1,
| ||||
C、[-1,
| ||||
D、(-
|
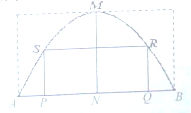 如图是一块外轮廓线(A,B间的曲线部分)为抛物线的钢板,MN为抛物线的对称轴,A,B是抛物线上关于MN对称的两点,其中AB=2,MN=1,先要将其割成矩形PQRS,使矩形的两个顶点P,Q落在线段AB上,另两个顶点R,S落在抛物线上.(1)建立适当的直角坐标系,求出这一抛物线的方程;
如图是一块外轮廓线(A,B间的曲线部分)为抛物线的钢板,MN为抛物线的对称轴,A,B是抛物线上关于MN对称的两点,其中AB=2,MN=1,先要将其割成矩形PQRS,使矩形的两个顶点P,Q落在线段AB上,另两个顶点R,S落在抛物线上.(1)建立适当的直角坐标系,求出这一抛物线的方程;