题目内容
 己知一个几何体的三视图如图.则该几何体的表面积为( )
己知一个几何体的三视图如图.则该几何体的表面积为( )A、6+2
| ||||
B、2+2
| ||||
C、6+2
| ||||
D、2+2
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:判断三视图复原的几何体的形状,利用三视图的数据求解几何体的表面积即可.
解答:
 解:由题意可知几何体是底面为边长为2正方形的四棱锥,棱锥的顶点在底面的射影是正方形的一边的中点.
解:由题意可知几何体是底面为边长为2正方形的四棱锥,棱锥的顶点在底面的射影是正方形的一边的中点.
棱锥的高为:2.如图:几何体的底面ABCD面积为:4.垂直底面的侧面PAD面积1×2=2,
侧面PAB与PCD面积为:2×
×2×
=2
.与垂直底面的侧面的对面PBC面积为:
×2×
=2
.
几何体的表面积为:6+2
+2
.
故选:A.
 解:由题意可知几何体是底面为边长为2正方形的四棱锥,棱锥的顶点在底面的射影是正方形的一边的中点.
解:由题意可知几何体是底面为边长为2正方形的四棱锥,棱锥的顶点在底面的射影是正方形的一边的中点.棱锥的高为:2.如图:几何体的底面ABCD面积为:4.垂直底面的侧面PAD面积1×2=2,
侧面PAB与PCD面积为:2×
| 1 |
| 2 |
| 5 |
| 5 |
| 1 |
| 2 |
| 22+22 |
| 2 |
几何体的表面积为:6+2
| 5 |
| 2 |
故选:A.
点评:本题考查三视图复原几何体的画法,表面积的求法,考查空间想象能力以及计算能力.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知θ是第一象限角,则方程x2+y2sinθ=1表示的图形是( )
| A、圆 | B、椭圆 |
| C、双曲线 | D、圆或椭圆 |
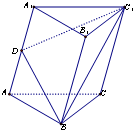 如图,三棱柱ABC-A1B1C1中,D是棱AA1的中点,平面BDC1分此棱柱为上下两部分,则这上下两部分体积的比为( )
如图,三棱柱ABC-A1B1C1中,D是棱AA1的中点,平面BDC1分此棱柱为上下两部分,则这上下两部分体积的比为( )| A、2:3 | B、1:1 |
| C、3:2 | D、3:4 |
已知矩形ABCD的顶点在半径为13的球O的球面上,且AB=8,BC=6,则棱锥O-ABCD的高为( )
| A、12 | B、13 | C、14 | D、5 |
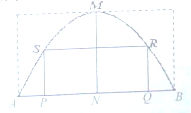 如图是一块外轮廓线(A,B间的曲线部分)为抛物线的钢板,MN为抛物线的对称轴,A,B是抛物线上关于MN对称的两点,其中AB=2,MN=1,先要将其割成矩形PQRS,使矩形的两个顶点P,Q落在线段AB上,另两个顶点R,S落在抛物线上.(1)建立适当的直角坐标系,求出这一抛物线的方程;
如图是一块外轮廓线(A,B间的曲线部分)为抛物线的钢板,MN为抛物线的对称轴,A,B是抛物线上关于MN对称的两点,其中AB=2,MN=1,先要将其割成矩形PQRS,使矩形的两个顶点P,Q落在线段AB上,另两个顶点R,S落在抛物线上.(1)建立适当的直角坐标系,求出这一抛物线的方程;