题目内容
复数z=（a2-2a）+（a2-a-2）2，对应点在虚轴上，则复数a= ．
考点：复数的代数表示法及其几何意义
专题：数系的扩充和复数
分析：直接由复数的实部等于0且虚部不等于0求得a的值．
解答：
解：∵复数z=（a2-2a）+（a2-a-2）i，对应点在虚轴上，
∴
，解得：a=0．
故答案为：0．
∴
|
故答案为：0．
点评：本题考查了复数的代数表示法及其几何意义，考查了复数是纯虚数的条件，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设a=sin（-810°），b=tan（
），c=lg
，则它们的大小关系为（ ）
| 33π |
| 8 |
| 1 |
| 5 |
| A、a＜b＜c |
| B、a＜c＜b |
| C、b＜c＜a |
| D、c＜a＜b |
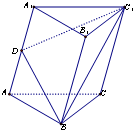如图，三棱柱ABC-A1B1C1中，D是棱AA1的中点，平面BDC1分此棱柱为上下两部分，则这上下两部分体积的比为（ ）| A、2：3 | B、1：1 |
| C、3：2 | D、3：4 |
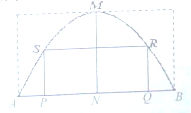如图是一块外轮廓线（A，B间的曲线部分）为抛物线的钢板，MN为抛物线的对称轴，A，B是抛物线上关于MN对称的两点，其中AB=2，MN=1，先要将其割成矩形PQRS，使矩形的两个顶点P，Q落在线段AB上，另两个顶点R，S落在抛物线上．（1）建立适当的直角坐标系，求出这一抛物线的方程；