题目内容

设函数f（x）=6x3（a+2）x2+2ax．
（1）若f（x）的两个极值点为x1，x2，且x1•x2=1，求实数a的值；
（2）是否存在实数a，使得f（x）是（-∞，+∞）上的单调函数？若存在，求出a的值；若不存在，说明理由．
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：（1）求出原函数的导函数，由根与系数关系列式求得实数a的值；
（2）由导函数恒有两个不等的实数根，说明导函数有两个极值点，则说明不存在实数a，使得f（x）是（-∞，+∞）上的单调函数．
解答： 解：（1）由f（x）=6x3（a+2）x2+2ax，得
f′（x）=18x2+6（a+2）x+2a，令f′（x）=0，得18x2+6（a+2）x+2a=0，
设其两根为x1，x2，
由x1•x2=
2a
18
=1，得a=9；
（2）∵f′（x）=18x2+6（a+2）x+2a，图象为开口向上的抛物线，
△=36（a+2）2-8×18a=36（a2+4）＞0，
∴方程18x2+6（a+2）x+2a=0有两个不等的实数根，
故不存在实数a，使得f（x）是（-∞，+∞）上的单调函数．
点评：本题考查了利用导数研究函数的单调性，考查了利用导数研究函数的极值，训练了一元二次方程的根与系数关系，是中档题．
练习册系列答案
相关题目
若圆锥的轴截面是正三角形，则它的侧面积是底面积的（　　）
A、4倍
B、3倍
C、
2
倍
D、2倍
（理做）已知函数f（x）=
1
x-1
-lnx，函数y=f（|x|）的零点个数为n，则n=（　　）
A、2B、4C、6D、8
（1）设x，y∈R，向量
a
=（x，1），
b
=（1，y），
c
=（2，-4），且
a
⊥
c
，
b
∥
c
，求|
a
+
b
|和
a
+
b
与
c
的夹角；
（2）设0为△ABC的外心，已知AB=3，AC=4，非零实数x，y满足
AO
=x
AB
+y
AC
且x+2y=1，则cos∠BAC的值．
设Sn为数列{an}的前n项之和，若不等式n2an2+4Sn2≥λn2a12对任何等差数列{an}及任何正整数n恒成立，则λ的最大值为
 
．
已知函数f（x）=|x+2|+1，g（x）=ax．若关于x的方程f（x）=g（x）有两个不相等的实根，则实数a的取值范围是（　　）
A、（-1，-
1
2
）
B、（
1
2
，1）
C、（0，
1
2
）
D、（-∞，-1）
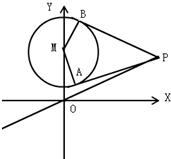如图，已知圆M：x2+（y-4）2=4，直线l的方程为x-2y=0，点P是直线l上一动点，过点P作圆的切线PA、PB，切点为A、B．
（1）当P的横坐标为
16
5
时，求∠APB的大小；
（2）求证：经过A、P、M三点的圆N必过定点，并求出所有定点的坐标．
下列式子正确的是（　　）
A、
AB
-
AC
=
BC
B、
a
•（
b
•
c
）=（
a
•
b
）•
c
C、λ（μa）=（λμ）
a
D、
O
•
AB
=
O
在△ABC中，已知25cos2A+120sin2
B+C
2
=17．
（1）求cosA的值；
（2）若a=4
2
，b=5，求向量
BA
在
BC
方向上的投影．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网