题目内容
1.将函数f(x)=ax+1(a>0,a≠1)的图象向右平移2个单位得到函数g(x)的图象,则( )| A. | 存在实数x0,使得g(x0)=1 | B. | 当x1<x2时,必有g(x1)<g(x2) | ||
| C. | g(2)的取值与实数a有关 | D. | 函数g(f(x))的图象必过定点 |
分析 根据函数平移以及变化规律,求得g(x)的解析式,再逐一判断各个选项是否正确,从而得出结论.
解答 解:将函数f(x)=ax+1(a>0,a≠1)的图象向右平移2个单位得到函数g(x)=ax-2 +1的图象,
由于 ax-2 >0,故不存在实数x0,使得g(x0)=1,故排除A;
由于a的范围不能进一步确定,故不能判断g(x)=ax-2 +1的单调性,故排除B;
由于g(2)=2,它的取值与实数a无关,故排除C;
由于g[f(x)]=a[f(x)-2]+1,故当x=0时,f(x)=2,g[f(x)]=a0+1=2,故D正确,
故选:D.
点评 本题主要考查了函数平移以及变化规律:左加右减,上加下减,属于基础题.

练习册系列答案
相关题目
12.已知O是三角形ABC所在平面内一点,且满足$\overrightarrow{BA}$•$\overrightarrow{OA}$+$\overrightarrow{BC}$2=$\overrightarrow{AB}$•$\overrightarrow{OB}$+$\overrightarrow{AC}$2,则点O在( )
| A. | AB边中线所在的直线上 | B. | ∠C平分线所在的直线上 | ||
| C. | 与AB垂直的直线上 | D. | 三角形ABC的外心 |
9.执行如下框图所示算法,若实数a、b不相等,依次输入a+b,a,b,输出值依次记为f(a+b),f(a),f(b),则f(a+b)-f(a)-f(b)的值为( )

| A. | 0 | B. | 1或-1 | C. | 0或±1 | D. | 以上均不正确 |
11.设l、m是两条不同的直线,α是一个平面,则下列说法正确的是( )
| A. | 若l⊥m,m⊆α则l⊥α | B. | 若l∥α,m⊆α则l∥m | C. | 若l⊥α,l∥m则m⊥α | D. | 若l∥α,m∥α则l∥m |
6.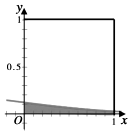 在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )
在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )
附:若X:N(μ,δ2),则P(μ-δ<X≤μ+δ)=0.6826.P(μ-δ<X≤μ+2δ)=0.9544.
 在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )
在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )附:若X:N(μ,δ2),则P(μ-δ<X≤μ+δ)=0.6826.P(μ-δ<X≤μ+2δ)=0.9544.
| A. | 906 | B. | 1359 | C. | 2718 | D. | 3413 |
6.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=1+2i,i为虚数单位,则z1z2=( )
| A. | 1-2i | B. | -5 | C. | 5 | D. | 5i |