题目内容
6.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=1+2i,i为虚数单位,则z1z2=( )| A. | 1-2i | B. | -5 | C. | 5 | D. | 5i |
分析 利用复数的运算法则与共轭复数的定义、几何意义即可求出答案.
解答 解:∵复数z1,z2在复平面内的对应点关于虚轴对称,z1=1+2i,
∴z2=-1+2i.
∴z1•z2=(1+2i)(-1+2i)=-5.
故选:B.
点评 本题考查了复数的运算法则与共轭复数的定义、几何意义,属于基础题.

练习册系列答案
相关题目
1.将函数f(x)=ax+1(a>0,a≠1)的图象向右平移2个单位得到函数g(x)的图象,则( )
| A. | 存在实数x0,使得g(x0)=1 | B. | 当x1<x2时,必有g(x1)<g(x2) | ||
| C. | g(2)的取值与实数a有关 | D. | 函数g(f(x))的图象必过定点 |
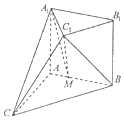 如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.
如图,在多面体ABCA1B1C1中,四边形ABB1A1是正方形,CA⊥平面ABB1A1,AC=AB=1,B1C1∥BC,BC=2B1C1.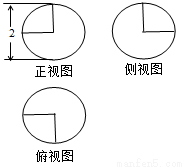
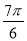 B.
B.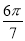 C.
C.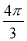 D.
D.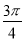
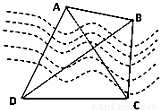
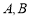 两点都在河的对岸(不可到达),为了测量
两点都在河的对岸(不可到达),为了测量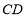 ,测得:
,测得: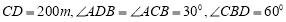 ,则
,则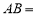 ()
()
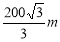 B.
B.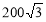
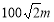 D.数据不够,无法计算
D.数据不够,无法计算