题目内容
12．在区间[-1，2]上随机取一个数x，则0≤x≤1的概率为$\frac{1}{3}$．分析 利用几何槪型的概率公式，求出对应的区间长度，利用长度比求概率．
解答 解：在区间[-1，2]上随机选取一个数x，则0≤x≤1，
则0≤x≤1的概率概率$\frac{1-0}{2+1}$=$\frac{1}{3}$，
故答案为：$\frac{1}{3}$
点评 本题主要考查了几何概型，简单地说，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
练习册系列答案
阅读快车系列答案
相关题目
4．
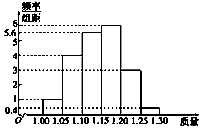为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：kg），并将所得数据分组，画出频率分布直方图（如图所示）．
（1）在下面表格中填写相应的频率；
（2）估计数据落在[1.15，1.30）中的概率为多少；
（3）将上面捕捞的100条鱼分别作一记号后再放回水库．几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条．请根据这一情况来估计该水库中鱼的总条数．
为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：kg），并将所得数据分组，画出频率分布直方图（如图所示）．（1）在下面表格中填写相应的频率；
| 分组 | 频率 |
| [1.00，1.05） | |
| [1.05，1.10） | |
| [1.10，1.15） | |
| [1.15，1.20） | |
| [1.20，1.25） | |
| [1.25，1.30） |
（3）将上面捕捞的100条鱼分别作一记号后再放回水库．几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条．请根据这一情况来估计该水库中鱼的总条数．
7．某校高一年级有甲、乙、丙三位学生，他们第一次、第二次、第三次月考的物理成绩如表：
则下列结论正确的是（ ）
| 第一次月考物理成绩 | 第二次月考物理成绩 | 第三次月考物理成绩 | |
| 学生甲 | 80 | 85 | 90 |
| 学生乙 | 81 | 83 | 85 |
| 学生丙 | 90 | 86 | 82 |
| A． | 甲、乙、丙第三次月考物理成绩的平均数为86 | |
| B． | 在这三次月考物理成绩中，甲的成绩平均分最高 | |
| C． | 在这三次月考物理成绩中，乙的成绩最稳定 | |
| D． | 在这三次月考物理成绩中，丙的成绩方差最大 |
1．将函数f（x）=ax+1（a＞0，a≠1）的图象向右平移2个单位得到函数g（x）的图象，则（ ）
| A． | 存在实数x0，使得g（x0）=1 | B． | 当x1＜x2时，必有g（x1）＜g（x2） | ||
| C． | g（2）的取值与实数a有关 | D． | 函数g（f（x））的图象必过定点 |