题目内容
已知函数 y=f(x)的值域是[-1,2],函数 y=f(-x)的值域为 ,函数 y=-f(x)的值域为 .
考点:函数的值域,函数的图象与图象变化
专题:规律型,数形结合
分析:考察函数的值域和图象的对称问题,可以转化为点对称理解.
如果y=f(x)上有一点(x,y),则y=f(-x)有一点(-x,y),两点关于y轴对称,则两函数图象关于y轴对称,值域相同,可以类比y=logax;
同理如果y=f(x)上有一点(x,y),则y=-f(x)有一点(x,-y),两点关于x轴对称,则两函数图象关于x轴对称,值域内的值互为相反数.
如果y=f(x)上有一点(x,y),则y=f(-x)有一点(-x,y),两点关于y轴对称,则两函数图象关于y轴对称,值域相同,可以类比y=logax;
同理如果y=f(x)上有一点(x,y),则y=-f(x)有一点(x,-y),两点关于x轴对称,则两函数图象关于x轴对称,值域内的值互为相反数.
解答:
解:y=f(x)与y=f(-x)图象关于y轴对称,值域相同,与y=-f(x)图象关于x轴对称,值域相反.
故函数 y=f(-x)的值域为[-1,2],函数 y=-f(x)的值域为[1,-2].
故函数 y=f(-x)的值域为[-1,2],函数 y=-f(x)的值域为[1,-2].
点评:本题考查函数图象的对称问题,总结如下:
y=f(x)与y=f(-x)关于y轴对称,参照偶函数f(x)=f(-x);
y=f(x)与y=-f(x)关于x轴对称;
y=f(x)与y=-f(-x)关于原点对称,参照奇函数f(-x)=-f(x);
y=f(x)与其反函数y=f-1(x)关于直线y=x对称.
y=f(x)与y=f(-x)关于y轴对称,参照偶函数f(x)=f(-x);
y=f(x)与y=-f(x)关于x轴对称;
y=f(x)与y=-f(-x)关于原点对称,参照奇函数f(-x)=-f(x);
y=f(x)与其反函数y=f-1(x)关于直线y=x对称.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“m<8”是“方程
-
=1表示双曲线”的( )
| x2 |
| m-10 |
| y2 |
| m-8 |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
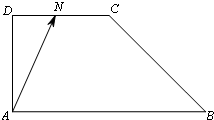 如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=
如图,在梯形ABCD中,AB∥DC,AD⊥AB,AD=DC=